 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Австрия >> 2001 >> Заключительный тур | Показать решения |
|
|
| Австрийская математическая олимпиада. 2001. Заключительный тур |
|
|
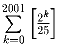 –
натуральное число ([x] – наибольшее целое число, не превосходящее x)
–
натуральное число ([x] – наибольшее целое число, не превосходящее x)Задача 2: Найдите все тройки натуральных чисел, являющиеся решениями системы уравнений:
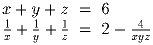
Задача 3:
Дан треугольник ABC, вписанный в окружность k(U,r). Рассмотрим окружность K(U,2r) и проведём к ней касательные a′, b′, c′ так, чтобы точка A лежала между a и a′, точка B лежала между b и b′, точка C лежала между c и c′. Теперь соединим середины сторон треугольника A1B1C1 с серединами соответствующих сторон треугольника ABC. Докажите, что получившиеся три отрезка пересекаются в одной точке.
Задача 4:
Найдите все функции 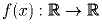 такие, что
f(f(x)² + f(y)) = xf(x) + y при всех x и y.
такие, что
f(f(x)² + f(y)) = xf(x) + y при всех x и y.
Задача 5:
Найдите все целые числа m, при которых все решения уравнения 3x³ – 3x² + m = 0 рациональны.
Задача 6:На отрезке AB, как на диаметре, построена полуокружность. На этой полуокружности взяты две точки C и D такие, что AC = CD. Касательная в точке C пересекает прямую BD в точке E. AE пересекает полуокружность в точке F. Докажите, что CF < FD.
| Задачная база >> Национальные зарубежные олимпиады >> Австрия >> 2001 >> Заключительный тур | Показать решения |