Задача 1:
В остроугольном треугольнике ABC проведены высоты AA′, BB′
и CC′, пересекающиеся в точке H. Точка H делит AA′
в отношении 1:1, а BB′ – в отношении 2:1. В каком отношении
точка H делит CC′?
Задача 2: а) Докажите, что 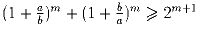 при любых
положительных a и b и любом натуральном m. В каком случае
достигается равенство?
при любых
положительных a и b и любом натуральном m. В каком случае
достигается равенство?
б) Докажите, что 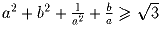 при любых
вещественных ненулевых значениях a и b.
В каком случае достигается равенство?
при любых
вещественных ненулевых значениях a и b.
В каком случае достигается равенство?
Задача 3: В последовательности an = a0,a1,a2, …
an + 1 = 10an + ( – 1)n при n ≥ 0. Известно, что a3 = 91.
Сколько элементов этой последовательности являются
точными квадратами?


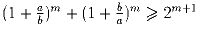 при любых
положительных a и b и любом натуральном m. В каком случае
достигается равенство?
при любых
положительных a и b и любом натуральном m. В каком случае
достигается равенство?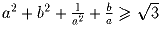 при любых
вещественных ненулевых значениях a и b.
В каком случае достигается равенство?
при любых
вещественных ненулевых значениях a и b.
В каком случае достигается равенство?