 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Болгария >> 1999 >> 3 тур | Показать решения |
|
|
| Болгарская математическая олимпиада.. 1999. 3 тур |
|
|
Найдите все тройки натуральных чисел (x,y,z) такие, что y – простое число, z не делится ни на y, ни на 3 и x³ – y³ = z².
Задача 2:
Выпуклый четырехугольник площади S вписан в окружность, центр которой лежит внутри четырехугольника. Докажите, что площадь четырехугольника, вершины которого – проекции точку пересечения диагоналей на стороны исходного четырехугольника не превосходит S/2.
Задача 3:Соревнование оценивается 8 судьями, каждый из которых ставит учаснику + или – . Известно, что для любых двух участников двое судей поставили + , двое – + первому и – второму, двое – – первому и + второму, и двое обоим поставили – . Определите максимально возможное количество участников.
Задача 4:Решите уравнение в целых числах: x³ = y³ + 2y² + 1.
Задача 5:
На сторонах AC и AB треугольника ABC выбрали точки B1 и C1 соответственно. D – точка пересечения BB1 и CC1. Докажите, что четырехугольник AB1DC1 вписанный тогда и только тогда, когда окружности, вписанные в треугольники ABD и ACD касаются.
Задача 6:Равносторонний треугольник со стороной 1 покрыт 6 кругами
радиуса r. Докажите, что 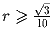 .
.
| Задачная база >> Национальные зарубежные олимпиады >> Болгария >> 1999 >> 3 тур | Показать решения |