 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Канада >> 1973 | Показать решения |
|
|
| Канадская математическая олимпиада.. 1973 |
|
|
(i) Решите систему неравенств 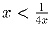 и x < 0.(ii) Найдите наибольшее целое число, удовлетворяющее неравенствам 4x + 13 < 0
и x² + 3x > 16.(iii) Найдите рациональное число между 11/64 и 6/13.(iv) Представьте 100000 в виде произведения двух целых чисел ни одно
из которых не делится на 10.(v) Вычислите: 1/ ㏒ 236 + 1/ ㏒ 336.
и x < 0.(ii) Найдите наибольшее целое число, удовлетворяющее неравенствам 4x + 13 < 0
и x² + 3x > 16.(iii) Найдите рациональное число между 11/64 и 6/13.(iv) Представьте 100000 в виде произведения двух целых чисел ни одно
из которых не делится на 10.(v) Вычислите: 1/ ㏒ 236 + 1/ ㏒ 336.
Решите уравнение |x + 3| – |x – 1| = x + 1.
Задача 3:Докажите, что если p и p + 2 – простые числа большие 3, то p + 1 делитс на 6.
Задача 4:В выпуклом девятиугольнике P0P1 … P8 провели диагонали (см. рис.), которыми он разбился на 7 треугольников. Сколькими способами можно перенумеровать эти треугольники числами от 1 до 7 так, чтобы Pi были бы вершинами i-х треугольников?
Задача 5: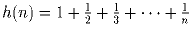 . Докажите, что
n + h(1) + h(2) + … + h(n – 1) = nh(n).
. Докажите, что
n + h(1) + h(2) + … + h(n – 1) = nh(n).
A и B – точки на окружности не лежащие на одной прямой с ее центром. XY – произвольный диаметр. Найдите геометрическое место точек P – точек пересечения прямых AX и BY.
Задача 7:Заметим, что 1/1 = 1/2 + 1/2; 1/2 = 1/3 + 1/6; 1/3 = 1/4 + 1/12; 1/4 = 1/5 + 1/20. Найдите закономерность и докажите ее. Также, докажите, что для любого n существуют числа i и j такие, что
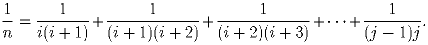
| Задачная база >> Национальные зарубежные олимпиады >> Канада >> 1973 | Показать решения |