 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Канада >> 1976 | Показать решения |
|
|
| Канадская математическая олимпиада.. 1976 |
|
|
Веса четырех гирь образуют геометрическую прогрессию. Как найти самую тяжелую из них за два взвешивания на чашечных весах?
Задача 2:a0 = 1, a1 = 2 и для любого n ≥ 1 n(n + 1)an + 1 = n(n – 1)an – (n – 2)an – 1. Найдите значение суммы:
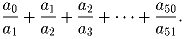
В шахматном турнире в один круг участвовало два семиклассника и несколько восьмиклассников. Семиклассники получили на двоих 8 очков, в то время как все восьмиклассники получили очков поровну. Сколько восьмиклассников могло участвовать в турнире? Найдите все возможные варианты. (в шахматах за победу дают 1, за ничью – 1/2, за проигрыш – 0 очков).
Задача 4:На диаметре AB окружности зафиксировали точку C, Q –
произвольная точка окружности, P – точка на прямой QC такая,
что 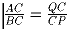 . Найдите геометрическое место точек
P. (???!!!???)
. Найдите геометрическое место точек
P. (???!!!???)
Докажите, что натуральное число n равно сумме не менее чем двух последовательных натуральных чисел тогда и только тогда, когда оно не является степенью 2.
Задача 6: A, B, C, D – точки в пространстве такие, что ∠ ABC = ∠ BCD = ∠ CDA = ∠ DAB = π /2. Докажите, что эти точки лежат в одной плоскости.
Задача 7:
P(x,y) – многочлен от двух переменных, такой, что P(x,y) = P(y,x) для всех x и y. Известно, что P(x,y) делится на (x – y). Докажите, что P(x,y) делится на (x – y)².
Задача 8:
Стороны и диагонали правильного 9-угольника покрасили в два цвета – синий и красный. Известно, что у любого треугольника, вершины которого совпадают с вершинами 9-угольника, по крайней мере одна сторона – красная. Докажите, что можно найти 4 вершины таких, что все стороны и диагонали получившегося четырехугольника будут красными.
| Задачная база >> Национальные зарубежные олимпиады >> Канада >> 1976 | Показать решения |