 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Канада >> 1977 | Показать решения |
|
|
| Канадская математическая олимпиада.. 1977 |
|
|
f(x) = x² + x. Докажите, что уравнение 4f(a) = f(b) не имеет натуральных решений.
Задача 2:
Точка A находится внутри круга с центром O. Найдите все точки P на окружности такие, что угол OPA максимальный.
Задача 3:
Найдите наименьшее основание системы счисления в которой число 777 является точной четвертой степенью.
Задача 4:
Все коэффициенты произведения двух многочленов с целыми коэффициентами четные, но не все из них делятся на 4. Докажите, что все коэффициенты одного из двух перемноженных многочленов четны, и по крайней мере один из коэффициентов второго нечетен.
Задача 5:
Через точку P у основания конуса провели наикратчайшую линию соединяющую P с собой. Найдите наименьшее расстояние от этой лини до вершины конуса, если радиус основания равен 1, а боковая сторона 3?
Задача 6:
0 < u < 1. Определим последовательность u1 = 1 + u,
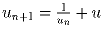 . Докажите, что un > 1 при всех n.
. Докажите, что un > 1 при всех n.
Город имеет форму прямоугольника m × n. Докажите, что количество способов пройти из северо-восточного угла города в юго-западный не проходя ни по какому перекрестку дважды не более чем 2mn.
| Задачная база >> Национальные зарубежные олимпиады >> Канада >> 1977 | Показать решения |