 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Канада >> 1983 | Убрать решения |
|
|
| Канадская математическая олимпиада.. 1983 |
|
|
Найдите все натуральные w,x,y,z, которые удовлетворяют уравнению w! = x! + y! + z!.
Решение:
Путь x ≤ y ≤ z. Поделив равенство на x! получим (x + 1) × … × w = 1 + (x + 1) × … × y + (x + 1) × … × z. Заметим, что если y > x, то 1 делитс на x + 1, чего быть не может. Следовательно y = x и, если x ≠ z, то 2 делится на x + 1, следовательно x = 1, но уравнение w! = 2 + z! не имеет решений. Тогда x = y = z и w! = 3x!, следовательно w = 3, x = y = z = 2.
Задача 2:
Tr – преобразование плоскости, которое точку (x,y) переводит в точку (2rx,r2rx + 2ry). Найдите все функции f графики которых не меняются при любом преобразовании Tr.
Решение:
Зафиксируем r. Тогда f(2rx) = r2rx + 2rf(x), в частности f(2r) = r2r + 2rf(1) и f( – 2r) = – r2r + 2rf( – 1). Функции, удовлетворяющие последним двум условиям – f(x) = x ㏒ 2x + ax при x > 0 и f(x) = x ㏒ 2|x| + bx, при x ≤ 0. Нетрудно видеть, что графики этих функций не меняются при всех преобразованиях Tr.
Задача 3:
Является ли объем тетраэдра функцией от площадей его граней?
Задача 4:
Докажите, что для любого простого p существует бесконечно много n таких, что 2n – n делится на p.
Решение:
Будем искать n в виде q(p – 1), тогда остаток от деления 2n на p будет равен 1. Осталось, чтобы остаток от деления q(p – 1) также был бы равен 1, для этого q должно иметь остаток p – 1, следовательно q = kp – 1 и искомые n = (kp – 1)(p – 1).
Задача 5:
Докажите, что среднее геометрическое чисел a1, … ,an равно среднему геометрическому средних геометрических всех непустых подмножеств a1, … ,an.
Решение:
Число ai входит в одно среднее в степени 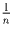 , во второе –
в степени
, во второе –
в степени
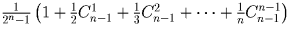 . нетрудно видеть, что вторая сумма равна
. нетрудно видеть, что вторая сумма равна 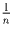
| Задачная база >> Национальные зарубежные олимпиады >> Канада >> 1983 | Убрать решения |