Задача 1: Докажите, что произведение первых n натуральных чисел делится на сумму первых n натуральных чисел в том и только том случае, когда n + 1 не является нечётным простым числом.

Задача 2: Для произвольных чисел x,y,z ≥ 0 докажите неравенство x(x – z)² + y(y – z)² ≥ (x – z)(y – z)(x + y – z) и определите, когда достигается равенство.

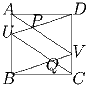
Задача 3: ABCD – квадрат, U и V – внутренние точки сторон AB и CD соответственно. P – точка пересечения отрезков AV и DU, Q – точка пересечения отрезков CU и BV. Определите все возможные способы выбрать U и V так, чтобы площадь четырёхугольника PUQV была максимальной.

Задача 4: Решите уравнение

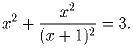
Задача 5: Колода из 2n + 1 карты состоит из джокера и по две карты помеченных каждым из натуральных чисел от 1 до n включительно. 2n + 1 карту положили в ряд так, что джокер оказался в середине. При этом для каждого k (1 ≤ k ≤ n) между двумя картами с числом k расположена ровно k – 1 карта. Определите все значения n, не превосходящие 10, при которых это возможно. При каких значениях n это невозможно?