 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Канада >> 1996 | Показать решения |
|
|
| Канадская математическая олимпиада.. 1996 |
|
|
α , β и γ – корни уравнения x³ – x – 1 = 0. Найдите
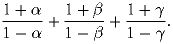
Задача 2:
Найдите все вещественные решения следующей системы уравнений:
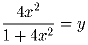
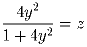
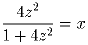
Задача 3:
a1, a2, , an – некоторая перестановка чисел 1, 2, , n. Через f(n) обозначим количество таких перестановок, что
Треугольник ABC – равнобедренный (AB = AC). Бисектрисса угла B пересекает отрезок AC в точке D и BC = BD + AD. Найдите ∠ A.
Задача 5:Дано m положительных рациональных чисел: r1, r2, , rm таких, что
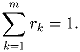
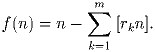
| Задачная база >> Национальные зарубежные олимпиады >> Канада >> 1996 | Показать решения |