 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Канада >> 2000 | Показать решения |
|
|
| Канадская математическая олимпиада.. 2000 |
|
|
В полдень Анна, Бет и Кармен начали бежать по круговой дорожке длиной триста метров, стартовав с одной точки. Каждая из них бежала с постоянной скоростью в одном из двух возможных направлений. Докажите, что, если скорость Анны отличается от скоростей двух других девочек, то в какой-то момент времени Анна будет на расстоянии не менее ста метров от каждой из соперниц (расстояние измеряется вдоль более короткой из двух дуг, разделяющих бегуний).
Задача 2:Перестановка чисел 1901,1902, … ,2000 – последовательность чисел a1,a2, … ,a100, в которой каждое из этих чисел встречается только один раз. Сфомируем последовательность частичных сумм такой перестановки:
s1 = a1,\;\;s2 = a1 + a2,\;\;s3 = a1 + a2 + a3,\; … \;,\;s100 = a1 + a2 + • s + a100.
Для скольких таких перестановок в последовательности s1, … ,s100 не будет членов, делящихся на 3?
Задача 3: Пусть A = (a1,a2, … ,a2000) – последовательность целых чисел из промежутка [ – 1000,1000]. Предположим, что сумма элементов A равна 1. Докажите, что можно выбрать непустую подпоследовательность A, сумма элементов которой равна нулю.Задача 4:
Пусть ABCD – выпуклый четырёхугольник с
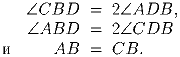
Предположим, что вещественные числа a1,a2, … ,a100 таковы, что
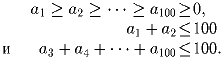
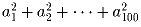 , и найдите все возможные
последовательности
a1,a2, … ,a100, для которых достигается этот максимум.
, и найдите все возможные
последовательности
a1,a2, … ,a100, для которых достигается этот максимум.
| Задачная база >> Национальные зарубежные олимпиады >> Канада >> 2000 | Показать решения |