Задача 1:

Ренди: Привет, Рейчел, ты написала интересное квадратное уравнение. Каковы его корни?

Рейчел: Его корнями являются два натуральных числа. Один из корней – мой возраст, другой – возраст моего младшего брата Джимми.

Ренди: Это очень изящно! Посмотрим, смогу ли я вычислить, сколько лет тебе и сколько Джимми. Это не должно быть сложным, ведь коэффициенты твоего уравнения – целые числа. Кстати, я заметил, что сумма всех трёх коэффициентов – простое число.

Рейчел: Интересно. Так посчитай, сколько мне лет.

Ренди: Вместо этого я попытаюсь угадать твой возраст и подставить его вместо x…Хм, получилось  – 55, а не 0.

Рейчел: Уйди, противный!

1. Докажите, что Джимми два года.
2. Определите возраст Рейчел

Задача 2:

Клетки на доске пронумерованы от  – 10 до 10, как показано на рисунке. Каждая клетка покрашена в красный или белый цвет, сумма чисел на красных клетках равна n. Морин положила жетон на клетку с номером 0. После этого она десять раз кидает монетку. Если выпадает орёл, Морин сдвигает жетон на одну клетку вправо, если решка, – то на одну клетку влево. Вероятность того, что после 10 бросков жетон окажется на красной клетке – рациональное число вида 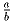. Известно, что a + b = 2001, определите максимальное возможное значение n.

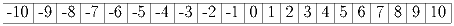
Задача 3: Дан треугольник ABC, у которого AC > AB. Пусть P – точка пересечения серединного перпендикуляра отрезка BC и биссекрисы  ∠ A. Постройте точку X на прямой AB и точку Y на прямой AC так, чтобы прямая PX была перпендикулярна прямой AB, а прямая PY перпендикулярна прямой AC. Пусть Z – точка пересечения XY и BC. Найдите отношение BZ:ZC.

Задача 4: Пусть n – натуральное число. У Ненси есть прямоугольная таблица, состоящая из натуральных чисел. Разрешается делать следующие ходы:

1. выбрать строку и умножить все числа, стоящие в ней на n;
2. выбрать строку и уменьшить все числа, стоящие в ней на n.

Найдите все возможные значения n, при которых верно следующее утверждение:

Какая бы ни была прямоугольная таблица, Ненси сможет через конечное число ходов добиться, чтобы все числа в таблице были равны 0.

Задача 5: Точки P₀, P₁, P₂ лежат на окружности радиуса 1, причём P₁P₂ = t < 2. Для каждого i ≥ 3, обозначим P_i центр описанной окружности  ∆ P_i – 1P_i – 2P_i – 3.

1. Докажите, что точки P₁,P₅,P₉,P₁₃, …  лежат на одной прямой.
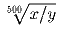2. Пусть x – расстояние между точками P₁ и P₁₀₀₁, а y – расстояние между точками P₁₀₀₁ и P₂₀₀₁. Найдите все значения t при которых  – целое число.