Задача 1: Пусть p – фиксированное простое число. Найти все пары
положительных целых чисел (x,y), удовлетворяющие уравнению p(x – y) = xy.
Задача 2: При каких положительных вещественных числах x выражение
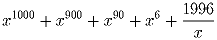
принимает наименьшее значение?
Задача 3: Равносторонний треугольник поворачивают вокруг его центра на угол
30. Найти площадь общей части исходного и полученного в
результате поворота треугольника, если длина стороны треугольника равна 1.
Задача 4: Доказать, что для любого простого числа p > 5 найдетс
положительное число n такое, что последние три цифры в десятичной
записи числа pn равны 001.
Задача 5: В пространстве расположены n (не обязательно правильных) тетраэдров
так, что у любых двух из них найдутся две общие вершины и никакие три из
этих тетраэдров не имеют двух общих вершин. Найти наибольшее возможное
значение числа n.