 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Грузия >> 1995 >> 9 | Показать решения |
|
|
| Грузинская математическая олимпиада. 1995. 9 |
|
|
Трехзначное число уменьшают на сумму цифр, полученное число опять, и т.,д. Докажите, что вне зависимости от исходного числа через 100 таких операций получится 0. Определите минимальное количество необходимых операций.
Задача 2:
На первой из двух одинаковых окружностей отметили семь дуг по 3 каждая, а на второй – десять дуг по 2. Докажите, что окружности можно наложить друг на друга так, что отмеченные дуги не будут пересекаться. Будет ли результат прежним, если на второй окружности отметить 11 дуг?
Задача 3:
Дано три положительных числа произведение которых равно 1. Докажите, что если их сумма больше суммы их обратных величин, то среди этих чисел не больше одного превосходящего 1.
Задача 4:
Докажите, что в любом выпуклом шестиугольнике существует такая
диагональ, которая отсекает треугольник с площадью не превосходящей
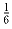 площади шестиугольника.
площади шестиугольника.
Задача 5:
Отметили некоторые целые числа, притом, для любых двух отмеченных чисел a и b число a + 2b также отмечено. Известно, что отмечены как положительные так и отрицательные числа. Докажите, что для любых трех отмеченных чисел a,b и c число a + b – c также отмечено.
| Задачная база >> Национальные зарубежные олимпиады >> Грузия >> 1995 >> 9 | Показать решения |