 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Иран >> 1994 | Показать решения |
|
|
| Иранская математическая олимпиада.. 1994 |
|
|
p – простое число, большее 3. Докажите, что 7p – 6p – 1 делится на 43.
Задача 2:
ABC – остроугольный треугольник, стороны и площадь которых равны a, b, c и S соответственно. Докажите, что необходимым и достаточным условием существования точки P расстояния от которой до вершин треугольника равны x, y и z является существование трех треугольников таких, что стороны первого равны x, y, a, второго – x, z, c, третьего – y, z, b, сумма площадей которых равна S.
Задача 3:
Для фиксированных n и r найдите минимальное m такое, что при любом
разбиении множества натуральных чисел от 1 до m на r частей в одной из
частей разбиения можно будет выбрать два числа a и b такие, что
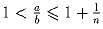 .
.
Задача 4:
В n-вершинном графе любые две вершины соединены путем длины не более 2. a) Найдите наименьшее количество ребер в таком графе. b) Какое количество ребер необходимо добавить к 6-вершинному циклу так, чтобы выполнялось предыдущее условие?
Задача 5:
Докажите, что для любых двух винтовых линий существует бесконечно много прямых равноудаленных от них.
Задача 6:
f(x) и g(x) – многочлены с вещественными коэффициентами, притом существует
бесконечно много рациональных x для которых отношение 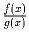 рационально. Докажите, что
рационально. Докажите, что 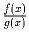 можно записать в виде отношения двух
многочленов с рациональными коэффициентами.
можно записать в виде отношения двух
многочленов с рациональными коэффициентами.
| Задачная база >> Национальные зарубежные олимпиады >> Иран >> 1994 | Показать решения |