Задача 1: a) Докажите, что для любого натурального n существуют различные натуральные числа x и y такие, что x + j делится на y + j при всех j от 1 до n b)  Докажите, что если x + j делится на y + j для любого натурального j, то x = y

Задача 2: Даны две концентрические окружности, радиусы которых относятся как 1:3. Докажите, что ортоцентр любого треугольника, вписанного в большую окружность лежит внутри меньшей, и наоборот, что любая точка, лежащая внутри меньшей окружности является ортоцентром некоторого треугольника, вписанного в большую.

Задача 3: Решите систему уравнений в вещественных числах:

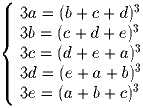
Задача 4: Найдите количество троек (A,B,C) подмножеств n-элементного множества таких, что A "— подмножество B, а B "— собственное подмножество C.

Задача 5: Последовательность A_n определена следующим образом: a₁ = 1, a₂ = 2 и a_n + 2 = 2a_n + 1 – a_n + 2 при n ≥ 1. Докажите, что для любого m число a_ma_m + 1 является членом этой последовательности.

Задача 6: В 3n клетках таблицы 2n × 2n расставлены нули, а в остальных "— единицы. Докажите, что все нули можно удалить вычеркнув n строк и n столбцов.