Задача 1:
В выпуклом четырехугольнике ABCD: ∠ BAC = 50,
∠ CAD = 60, ∠ CBD = 30,
∠ BDC = 25, E – точка пересечения диагоналей.
Найдите ∠ AEB.
Задача 2:
Сумма квадратов n простых чисел, каждое из которых больше 5
делится на 6. Докажите, что и n тоже делится на 6.
Задача 3:
Докажите, что для любого натурального n:
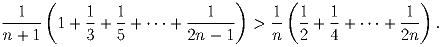
Задача 4:
В равнобедренном треугольнике ABC угол при вершине равен 30.
Точки A′,B′C′ получаются отражением вершин относительно противоположных
сторон. Докажите, что треугольник A′B′C′ равносторонний.
Задача 5:
Какое наименьшее значение может принимать
20 не обязательно различных
натуральных чисел с суммой 801.
Задача 6:
Дано 7-элементное множество A. Придумайте набор троек элементов A
такой, что любая пара элементов A принадлежит ровно одной тройке
набора.


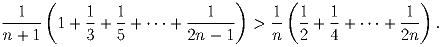
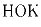 20 не обязательно различных
натуральных чисел с суммой 801.
20 не обязательно различных
натуральных чисел с суммой 801.