 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Ирландия >> 1995 | Показать решения |
|
|
| Ирландская математическая олимпиада.. 1995 |
|
|
В классе n² учеников. Каждую неделю они участвуют в соревновании, для которого их учитель разделяет на n команд по n учеников в каждой. Если это возможно, учитель разбивает учеников на команды таким способом, чтобы любые двое, однажды игравшие в одной команде, были бы в разных командах во все последующее время. Докажите, что по крайней мере после n + 2 недель какие-то два ученика по крайней мере дважды будут в одной команде.
Задача 2:Найдите все такие целые a, для которых уравнение x² + axy + y² = 1 имеет бесконечно много целочисленных решений.
Задача 3:Точки A,X,D лежат на одной прямой, притом X находится между A
и D. B – некоторая точка плоскости такая, что ∠ ABX больше
120. На отрезке BX взяли точку C. Докажите, что
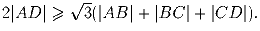
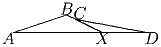
Задача 4:
Для каждого целого k пусть Xk обозначает точку с координатами (k,0). В некоторых точках Xk стоят фишки (возможно несколько в одной точке). За ход разрешается из любой точки Xj, где находится более одной фишки, взять 2 фишки и поместить одну из них на Xj – 1, другую на Xj + 1. В точке X0 лежит 2n + 1 фишка. Докажите, что вне зависимости от того как ходить через n(n + 1)(2n + 1)/6 ходов игра закончиться тем, что останется по одной фишке в каждой из точек X – n, … ,Xn.
Задача 5:Найдите все вещественнозначные функции f удовлетворяющие соотношению xf(x) – yf(y) = (x – y)f(x + y) для любых вещественных x и y
Задача 6:Докажите, что для любого натурального n справедливо неравенство nn ≤ (n!)² ≤ ((n + 1)(n + 2)/6)n.
Задача 7:a,b,c – комплексные числа такие, что все корни многочлена x³ + ax² + bx + c по модулю равны 1. Докажите, что тогда все корни многочлена x³ + |a|x² + |b|x + |c| также по модулю равны 1.
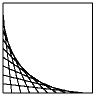
Задача 8:Пусть S – единичный квадрат на плоскости (0 ≤ x,y ≤ 1). Для каждого t такого, что 0 < t < 1 через Ct обозначим
множество точек из S лежащих над отрезком соединяющим точки (t,0) и
(0,1 – t) или на нем. Докажите, что всем Ct принадлежат те и только те
точки S, которые лежат над графиком кривой 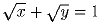 или на
нем.
или на
нем.
Задача 9:
С помощью циркуля и линейки восстановите треугольник ABC по трем точкам P, Q и R таким, что P – середина BC, Q лежит на стороне AC и |CQ|/|QA| = 2, R лежит на AB и |AR|/|RB| = 2.
Задача 10:Для каждого натурального n = p1p2p3p4, где pi различные простые числа, выпишем все 16 делителей n в порядке возрастания: 1 = d1 < d2 < d3 < • s < d15 < d16 = n. Докажите, что если n < 1995, то d9 – d8 ≠ 22.
| Задачная база >> Национальные зарубежные олимпиады >> Ирландия >> 1995 | Показать решения |