 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Ирландия >> 1996 | Показать решения |
|
|
| Ирландская математическая олимпиада.. 1996 |
|
|
Для каждого натурального n через f(n) обозначим наибольший общий делитель n! + 1 и (n + 1)!. Найдите чему равно f(n).
Задача 2:Для каждого натурального n через S(n) обозначим сумму цифр n в десятичной системе счисления. Докажите, что для любого n S(2n) ≤ 2S(n) ≤ 10S(2n). Докажите также, что существует такое n, что S(n) = 1996S(3n).
Задача 3:Пусть K = [0,1] и f – функция из K в множество вещественных чисел, удовлетворяющая следующим трем свойствам:
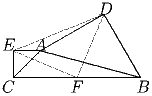
Точка F – середина стороны BC треугольника ABC. На сторонах AB и AC внешним образом построены равнобедренные прямоугольные треугольники ABD и ACE с прямыми углами D и E. Докажите, что треугольник FDE – равнобедренный и прямоугольный.
Задача 5:
Придумайте способ как разрезать квадрат на не менее чем пять частей из которых можно было бы сложить три попарно различных квадрата.
Задача 6:Последовательность чисел Фибоначчи F0,F1,F2, …
определяется следующим образом: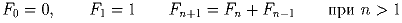 Докажите, что
Докажите, что
Докажите, что при всех натуральных n
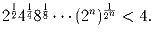
p – простое число, a и n – натуральные числа. Докажите, что если 2p + 3p = an, то n = 1.
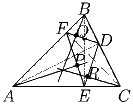
Задача 9:ABC – остроугольный треугольник. D,E,F – основани высот опущенных на стороны BC, CA и AB соответственно. P, Q и R – основания перпендикуляров опущенных из точек A, B, C на прямые EF, FD и DE соответственно. Докажите, что прямые AP, BQ и CR пересекаются в одной точке.
Имеется прямоугольная доска 5 × 9 клеток. Двое играют на ней в следующую игру:Первоначально на доске расположено несколько фишек, притом на каждой клетке стоит не более одной фишки. Ход заключается в перемещении всех фишек по следующим правилам:
| Задачная база >> Национальные зарубежные олимпиады >> Ирландия >> 1996 | Показать решения |