Задача 1:

Пусть S – множество всех чисел вида a(n) = n² + n + 1, где n – натуральное число. Докажите, что произведение a(n)a(n + 1) принадлежит S при всех натуральных n. Приведите (с доказательством) пример такой пары элементов s,t ∈ S, что .

Задача 2: Пусть ABCD –правильный пятиугольник, стороны которого равны 1, F – середина AB, а G и H – точки на сторонах CD и DE соответственно такие, что  ∠ GFD =  ∠ HFD = 30. Докажите, что треугольник GFH равнобедренный.

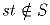В треугольник GFH вписан квадрат так, что одна из его сторон лежит на GH. Докажите, что FG имеет длину

а сторона квадрата равна

Задача 3: f(x) = 5x¹³ + 13x⁵ + 9ax. Найдите наименьшее натураьное число a такое, что f(x) делится на 65 при любом целом x.

Задача 4: a₁ < a₂ <  … a_M – вещественные числа. a₁,a₂, … ,a_M называется Слабой арифметической прогрессией длины M, если существуют вещественные числа x₀, x₁, x₂,…, x_M и d такие, что x₀ ≤ a₁ ≤ x₁ ≤ a₂ ≤ x₂ ≤ a₃ ≤ x₃ …  ≤ a_M < x_M, и x_i + 1 – x_i = d для i = 0,1,2 … M – 1, то есть x₀,x₁,x₂, … ,x_M – арифметическая прогрессия.

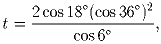
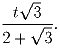
a) Докажите, что если a₁ < a₂ < a₃, то a₁,a₂,a₃ – слабая арифметическая прогрессия длины 3.

b) Пусть A – подмножество 0,1,2,3, … ,999 в которой не менее, чеи 730 членов. Докажите, что A содержит слабую арифметическую прогрессию длины 10.

Задача 5: Рассмотрим все параболы вида y = x² + 2px + q (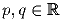), пересекающие оси абсцисс и ординат в трёх различных точках. Для каждой пары (p,q) обозначим через C_p,q окружность, проходящую через точки пересечения параболы y = x² + 2px + q с осями. Докажите, что все окружностями C_p,q имеют общую точку.

Задача 6: x и y – положительные вещественные числа, сумма которых равна 2. Докажите, что x²y²(x² + y²) ≤ 2

Задача 7: Пусть ABCD – вписанный четырёхугольник, R – радиус описанной окло него окружности, a, b, c и d – длины сторон четырёхугольника ABCD, Q – его площадь. Докажите, что

Выведите также, что

причём равенство достигается в том и только том случае, когда ABCD – квадрат.

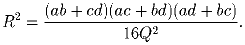
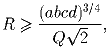
Задача 8: Для каждого натурального числа n найдите все такие натуральные m, что найдутся натуральные x₁ < x₂ <  …  < x_m, при которых

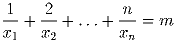
Задача 9: Докажите, что среди любых десяти последовательных целых чисел найдётся число взаимнопростое со всеми остальными.

Задача 10: Пусть p(x) = a₀ + a₁x +  …  + a_nxⁿ – многочлен с неотрицательными коэффициентами такой, что p(4) = 2, а p(16) = 8. Докажите, что p(8) ≤ 4 и найдите все такие многочлены p, что p(8) = 4.