 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Корея >> 1995 >> 1 тур | Убрать решения |
|
|
| Корейская математическая олимпиада.. 1995. 1 тур |
|
|
Конечное множество точек плоскости обладает тем свойством, что площадь треугольника с вершинами в данном множестве меньше 1. Докажите, что все множество можно поместить в треугольник площади меньше 4.
Задача 2:
Для данного натурального m найлите все тройки (x,y,n) натуральных чисел такие, что m и n взаимно просты и (x² + y²)m = (xy)n.
Решение:
Заметим, что простые делители x и y совпадают. Рассмотрим один из них – p. Пусть k и l – степени, в которых p входит в разложение x и y на простые множители. Покажем, что k = l. Если k < l, то в разложении левой части на простые множители p входит в степени 2km, правой части – в степени n(k + l), следовательно m > n. С другой стороны, по неравенству о среднем (x² + y²)m ≥ (2xy)m и m < n. Следовательно, x = y и уравнение принимает вид 2mx2m = x2n, откуда имеем, что при нечетном m уравнение не имеет решений. Если m – четное, что x = y = 2m/2, n = m + 1.
Задача 3:Около треугольника ABC описали окружность. Точки P, Q и R – середины дуг BC, CA, AB соответственно. Прямые AP, BQ, и CR пересекают BC, CA и AB в точках L, M и N соответственно. Докажите, что
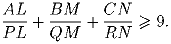
Задача 4:
Докажите, что количество разбиений числа n на m различных слагаемых равно количеству разбиений n – ½m(m + 1) на не более чем m слагаемых.
Задача 5:Найдите вероятность того, что три случайно выбранные на окружности точки лежат на одной полуокружности.
Задача 6:
Докажите, что любое натуральное число большее 1 можно представить в виде суммы нескольких не делящихся друг на друга слагаемых не имеющих простых делителей отличных от 2 и 3.
Решение:
Докажем по индукции. Числа 2 и 3 можно представить в таком виде. Допустим, что все числа меньше n также представимы в виде суммы не делящихся друг на друга слагаемых. Если n четное, то домножим представление для n/2 на 2. Очевидно, что полученное представление удовлетворяет условию. Для нечетного n пусть 3m – максимальная степень 3 не превосходящая n. Тогда n – 3m – четное число. В представлении n – 3m все слагаемые четные, притом ни одно из них не делится на 3m (иначе, если в разложении имеется слагаемое 23m + β с α > 0, то n ≤ 23m + β + 3m ≤ 3m + 1 и 3m – не максимальная степень 3, не превосходящая n). Таким образом, искомое представление получено.
Задача 7:Найдите все функции, заданные на всей вещественной оси, за исключением 0,
которые удовлетворяют условию 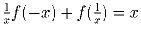 .
.
Задача 8:
Окружности O1 и O2 радиусов r1 и r2 (r1 < r2) соответственно пересекаются в точках A и B. Точка P лежит на окружности O1. Прямые PA и PB пересекают окружность O2 в точках Q и R соответственно. a) Выразите QR через r1,r2 и θ = ∠ APB. b) Докажите, что окружности O1 и O2 перпендикулярны тогда и только тогда, когда QR = 2r2.
| Задачная база >> Национальные зарубежные олимпиады >> Корея >> 1995 >> 1 тур | Убрать решения |