Задача 1:
Даны два различных натуральных числа a и b. Докажите, что существует
бесконечно много n таких, что a + n и b + n взаимно просты.
Задача 2:
Существует ли такая функция f определенная на множестве вещественных чисел, такая,
что f(f(x)) = x и f(f(x) + 1) = 1 – x для любого x?
Задача 3:
Даны окружность ω с центром в точке O и не пересекающая ее
прямая t. Точка E – проекция O на t. Из точки M на t,
отличной от E провели касательные к ω – MA и MB.
AB пересекает OE в точке X. Докажите, что положение точки
X не зависит от выбора M.
Задача 4: Числа a и b – положительные, n – натуральное. Докажите, что
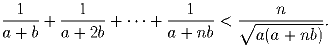
Задача 5:
Найдите наименьшее n обладающее следующим свойством: если из 9
попарно незнакомых людей выбрать n пар, и в каждую пару
сделать либо друзьями либо врагами, то из всей группы можно
будет выбрать либо тройку попарных друзей, либо тройку попарных врагов.