 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Испания >> 1991 | Показать решения |
|
|
| Испанская математическая олимпиада.. 1991 |
|
|
В прямоугольной системе координат на плоскости отметили все точки с целочисленными координатами (m,n). Затем соединили отрезками все те отмеченные точки, расстояние между которыми выражается целым числом. Докажите, что никакие два из полученных отрезков не пересекаются под углом 45°. Верно ли, что если провести аналогичные построения в пространстве, то найдутся два отрезка угол между которыми будет 45°?
Задача 2:a и b – два целых числа, отличных от 0, 1 и – 1. Рассмотрим матрицу:
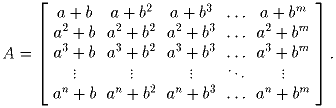
Задача 3:
Каким условиям должны удовлетворять коэффициенты u, v и w многочлена x³ – ux² + vx – w, чтобы из отрезков, длины которых равны корням многочлена можно было бы составить треугольник?
Задача 4:
A′, B′ и C′ – точки касания окружности, вписанной в треугольник ABC, со сторонами BC, CA и AB соответственно. D – точка пересечения бисектриссы угла A и прямой C′A′. Найдите все возможные значения, которые может принимать угол ADC.
Задача 5:
Для любого натурального числа n определим s(n) – количество чисел в записи числа n в двоичной системе счисления. Вычислите: σ (k) = s(1) + s(2) + s(3) + • s + s(2k).
Задача 6:Вычислите целую часть суммы:
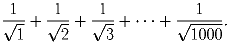
| Задачная база >> Национальные зарубежные олимпиады >> Испания >> 1991 | Показать решения |