 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Испания >> 1993 | Показать решения |
|
|
| Испанская математическая олимпиада.. 1993 |
|
|
На собрание приехал 201 человек из 5 стран. Среди каждых 6 из них найдется двое одинакового возраста. Докажите, что из некоторой страны на собрание приехало не менее 5 человек одного пола и одного возраста.
Задача 2:
Записан следующий арифметический треугольник:

Каждое число в треугольнике равно сумме двух стоящих над ним (таким образом в каждом последующем ряду на одно число меньше чем в предыдущем и последний ряд содержит всего лишь одно число). Докажите, что число, стоящее в последнем ряду делится на 1993
Задача 3:Докажите, что в произвольном треугольнике диаметр вписанной ок-руж-ности не превосходит радиуса описанной окружности.
Задача 4:Докажите, что для любого простого числа p отличного от 2 и 5 существует бесконечно много чисел делящихся на p десятичная запись которых содержит только единицы (111 … 1).
Задача 5:Рассмотрим 16 точек, образующих следующую решетку:

1) Сколько существует всего таких фигур?
2) Сколько из этих фигур неравных (в геометрическом смысле)?
3) Пусть каждая точка задана координатами (Xi,Yi). Докажите, что сумма по всем шести парам точек |Xi – Xj| + |Yi – Yj| не зависит от выбора четверки точек с вышеупомянутыми свойствами.
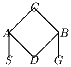
Задача 6:На рисунке изображен игральный автомат в казино. В начале игры в точке S появляется шарик. С каждым ходом игрока, шарик случайным образом перекатывается в одну из соседних точек, при этом в любой соседней точке он может оказаться с равной вероятностью. Игра заканчивается в случае если шарик обратно вернется в S, и тогда игрок проигрывает, или шарик окажется в точке G, и тогда игрок выигрывает. Найдите вероятность победы игрока и ожидаемое время игры.
| Задачная база >> Национальные зарубежные олимпиады >> Испания >> 1993 | Показать решения |