 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Испания >> 1996 | Показать решения |
|
|
| Испанская математическая олимпиада.. 1996 |
|
|
Два натуральных числа a и b таковы, что число
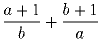 – целое. Докажите, что
наибольший общий делитель a и b не больше
– целое. Докажите, что
наибольший общий делитель a и b не больше 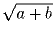 .
.
Задача 2:
G – центр тяжести треугольника ABC. Докажите, что если AB + GC = AC + GB, то треугольник ABC – равнобедренный.
Задача 3:a, b и c – три вещественных числа. Рассмотрим два квадратных трехчлена f(x) = ax² + bx + c и g(x) = cx² + bx + a. Известно, что |f( – 1)| ≤ 1, |f(0)| ≤ 1 и |f(1)| ≤ 1. Докажите что при – 1 ≤ x ≤ 1|f(x)| ≤ 5/4 и |g(x)| ≤ 2.
Задача 4:При каких вещественных значениях p существуют вещественные решени
уравнения 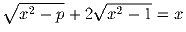 ? Решите уравнение для таких p.
? Решите уравнение для таких p.
Задача 5:
16 секретных агентов было заброшено в Port Aventura. Каждый из них следит за некоторыми из своих коллег. Известно, что если агент A следит за агентом B, то агент B не следит за агентом A. Любые 10 агентов могут быть перенумерованы таким образом, что первый будет следит за вторым, второй за третьим, …, десятый за первым. Докажите, что таким же образом можно занумеровать некоторых 11 агентов.
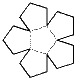
Задача 6:Следующая фигура составлена из 6 правильных пятиугольников со стороной 1 метр. Затем мы сгибаем ее по пунктирным линиям до совмещени сплошных линий. Найдите максимальный объем жидкости который можно налить в полученный «сосуд».
| Задачная база >> Национальные зарубежные олимпиады >> Испания >> 1996 | Показать решения |