Задача 1: a0 – целое число большее 2. Последовательность a0,a1,a2, …
строится следующим образом: an + 1 = an(1 + an), если an нечетно и
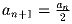 , если an четно. Докажите, что существует такое
число p, что ap > ap + 1 > ap + 2.
, если an четно. Докажите, что существует такое
число p, что ap > ap + 1 > ap + 2.
Задача 2: Натуральное число называется почти треугольным, если оно треугольное, либо
равно сумме различных треугольных чисел. Найдите количество почти
треугольных чисел не превосходящих 1997.
Задача 3: При каких n на доске n × n можно расставить n² неотрицательных чисел так,
чтобы число в каждой клетке равнялось бы разности каких-то двух своих соседей?
Задача 4: При помощи циркуля и линейки впишите в данный остроугольный треугольник ABC
равносторонний треугольник с вершинами D, E, F лежащими на сторонах
BC, AC, AB соответственно такой, что перпендикуляры восстановленные
к сторонам BC, AC и AB в этих точках пересекаются в одной точке.


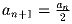 , если an четно. Докажите, что существует такое
число p, что ap > ap + 1 > ap + 2.
, если an четно. Докажите, что существует такое
число p, что ap > ap + 1 > ap + 2.