 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Польша >> 1993 >> 2 тур | Убрать решения |
|
|
| Польская математическая олимпиада.. 1993. 2 тур |
|
|
Докажите, что для любых положительных x,y,u и v
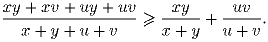
Дана окружность с центром O и точка P вне нее. Пусть l – прямая проходящая через точку P и пересекающая окружность в точках A и B. C – точка, симметричная A относительно прямой OP, а m – прямая, соединяющая точки B и C. Докажите, что при различных l все прямые m имеют общую точку.
Задача 3:
На ребре OA1 тетраэдра OA1B1C1 выбрали точки A2 и A3 такие, что OA1 > OA2 > OA3 > 0. На ребре OB1 выбрали точки B2,B3, а на ребре OC1 – точки C2 и C3 так, что плоскости A1B1C1, A2B2C2 и A3B3C3 параллельны. Vi – объем тетраэдра OAiBiCi, а V – объем тетраэдра OA1B2C3. Докажите, что V1 + V2 + V3 ≥ 3V.
Задача 4:
xn – последовательность натуральных чисел такая, что x1 = 1 и xn < xn + 1 ≤ 2n при n = 1,2, … Докажите, что для каждого натурального k существуют такие r и s, что xr – xs = k.
Задача 5:На сторонах BC, CA и AB треугольника ABC выбрали точки D, E и F соответственно, так, что радиусы окружностей вписанных в треугольники AEF, BFD и CFD равны r1. Радиусы окружностей вписанных в треугольники DEF и ABC соответственно равны r2 и r. Докажите что r1 + r2 = r.
Задача 6:Непрерывная вещественнозначная функция, определенная на всей вещественной оси, удовлетворяет соотношениям f(1000) = 999, и f(x)f(f(x)) = 1 для всех x. Найдите f(500).
| Задачная база >> Национальные зарубежные олимпиады >> Польша >> 1993 >> 2 тур | Убрать решения |