 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Польша >> 1994 >> 2 тур | Показать решения |
|
|
| Польская математическая олимпиада.. 1994. 2 тур |
|
|
Найдите все многочлены пятой степени P(x) с вещественными коэффициентами такие, что P(x) + 1 делится на (x – 1)³, а P(x) – 1 делится на (x + 1)³.
Задача 2:a1,a2, … ,an – положительные вещественные числа и
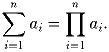
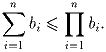
Сечение куба, проходящее через его центр – вписанный шестиугольник. Докажите, что он правильный.
Задача 4:В вершинах куба записаны числа 1 или – 1. На каждой грани записали произведение чисел в ее вершинах. Чему может быть равна сумма всех 14 чисел записанных на кубе?
Задача 5:Окружность, вписанная в треугольник ABC, касается его сторон AB и BC в точках P и Q соответственно. Докажите, что бисектрисса угла BAC перпендикулярна прямой SC, где S – точка пересечения бисектриссы с прямой PQ.
Задача 6:p – простое число. Докажите, что следующие два утверждени эквивалентны:
(1) существует такое целое n, что n² – n + 3 делится на p;
(2) существует такое целое m, что m² – m + 25 делится на p.
| Задачная база >> Национальные зарубежные олимпиады >> Польша >> 1994 >> 2 тур | Показать решения |