 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Польша >> 1994 >> 3 тур | Показать решения |
|
|
| Польская математическая олимпиада.. 1994. 3 тур |
|
|
Найдите все тройки положительных рациональных чисел таких, что
x + y + z, 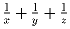 , xyz – натуральные числа.
, xyz – натуральные числа.
Даны две параллельные прямые k и l и окружность, не пересекающа прямую k. Из точки A, лежащей на k провели две касательных к окружности, которые пересекают прямую l в точках B и C. Пусть m – прямая проходящая через точку A и середину отрезка BC. Докажите что все такие прямые m (полученные при различном выборе точки A на k) проходят через одну точку.
Задача 3:Дано натуральное число c. Рассмотрим отображение w(A), которое
каждому подмножеству I = 1,2, … ,n сопоставляет
целое число от 1 до c, и для любых двух A и B (подмножеств
I) выполняется w(A ∩ B) = min (w(A),w(B)). Пусть
a(n) – число отображений удовлетворяющих вышеперечисленным свойствам.
Найдите 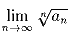 .
.
Задача 4: Имеется три сосуда. Емкость первого из них – m литров, второго – n литров, третьего – m + n литров, где числа m и n взаимно простыа. Третий сосуд полностью заполнен водой, в то время как первые два – пустые. Докажите, что переливаниями воды между сосудами можно добиться того, что в третьем сосуде будет ровно k литров воды, где k – произвольное число от 1 до m + n – 1. Задача 5:
A1,A2, … ,A8 – вершины параллелепипеда с центром в точке O. Докажите, что
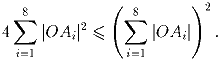
Различные вещественные числа x1,x2, … xn (n ≥ 4) удовлетворяют соотношениям:
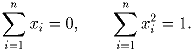
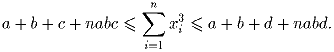
| Задачная база >> Национальные зарубежные олимпиады >> Польша >> 1994 >> 3 тур | Показать решения |