 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Польша >> 1997 >> 1 тур | Показать решения |
|
|
| Польская математическая олимпиада.. 1997. 1 тур |
|
|
Решите систему уравнений:
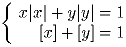
Внутри параллелограмма ABCD выбрали точку P такую, что ∠ ABP = ∠ ADP. Докажите, что ∠ PAB = ∠ PCB.
Задача 3:Докажите, что для любых вещественных чисел a,b ≥ 1, c ≥ 0 и для любого натурального n(ab + c)n – c ≤ ((b + c)n – c)an.
Задача 4:Докажите, что натуральное число n ≥ 2 составное тогда и только
тогда, когда существуют такие натуральные числа a, b, x, y, что
a + b = n и 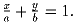
Бисектриссы углов A, B, C треугольника ABC пересекают противоположные стороны в точках D, E, F, а описанную окружность – в точках K, L и M соответственно. Докажите, что AD/DK + BE/EL + CF/FM ≥ 9.
Задача 6:
Многочлен P(x) степени n удовлетворяет следующим условиям: P(k) = k – 1 при k = 1,2,4,8, … ,2n. Найдите P(0).
Задача 7:Найдите точную верхнюю границу объемов тетраэдров, содержащихся в данном шаре, одно из ребер которого совпадает с диаметром шара.
Задача 8:an – число всех подмножеств множества 1,2, … ,6n, сумма элементов которых дает остаток 5 при делении на 6, а bn – число всех подмножеств множества 1,2, … ,7n, сумма элементов которых дает остаток 5 при делении на 7. Найдите отношение an/bn.
Задача 9:Найдите все функции f:\;[1, ∞ ) → [1, ∞ ) которые удовлетворяют следующим двум условиям:
(1) 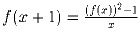 для всех x ≥ 1;
для всех x ≥ 1;
(2) функция g(x) = f(x)/x ограничена.
Задача 10:Внутри остроугольного треугольника ABC взяли точки P и Q такие, что ∠ ACP = ∠ BCQ и ∠ CAP = ∠ BAQ. Точки D, E и F – ортогональные проекции точки P на прямые BC, CA и AB соответственно. Докажите, что угол DEF прямой тогда и только тогда, когда точка Q является ортоцентром треугольника BDF.
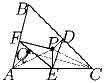
Задача 11:
Дано натуральное число m и отличный от нуля многочлен P(x) с целыми коэффициентами. Докажите что если P(x) имеет по крайней мере три различных целых корня, то многочлен P(x) + 5m имеет по крайней мере один целый корень.
Задача 12:На протяжении нескольких дней, ежедневно, трое из группы в n человек обедали вместе. Притом за это время каждые двое пообедали вместе ровно по одному разу. Докажите, что n дает остаток 1 или 3 при делении на 6.
| Задачная база >> Национальные зарубежные олимпиады >> Польша >> 1997 >> 1 тур | Показать решения |