 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Польша >> 1997 >> 3 тур | Показать решения |
|
|
| Польская математическая олимпиада.. 1997. 3 тур |
|
|
Натуральные числа x1,x2, … ,x7 удовлетворяют условиям: x6 = 144 и xn + 3 = xn + 2(xn + 1 + xn) при n = 1,2,3,4. Найдите x7.
Задача 2:Найдите все тройки вещественных чисел x,y,z которые удовлетворяют системе уравнений:
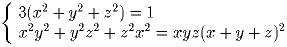
Медианы боковых граней ABD, ACD и BCD пирамиды ABCD проведенные из вершины D образуют равные углы с ребрами к которым они проведены. Докажите, что площадь каждой боковой грани меньше суммы площадей остальных боковых граней.
Задача 4:Последовательность a1,a2, … задана равенствами: a1 = 0, an = a[n/2] + ( – 1)n(n + 1)/2 при n > 1. Для каждого целого k ≥ 0 определите количество таких чисел n, что 2k ≤ n ≤ 2k + 1 и an = 0.
Задача 5:В выпуклом пятиугольнике ABCDE углы DCB и DEA прямые, а DC = DE. на отрезке AB взяли точку F такую, что AF:BF = AE:BC. Докажите, что ∠ FCE = ∠ ADE и ∠ FEC = ∠ BDC.
Задача 6:На окружности радиуса 1 взяли n различных точек. Пусть q –
количество отрезков с концами в этих точках длина которых больше 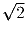 .
Докажите, что 3q ≤ n²
.
Докажите, что 3q ≤ n²
| Задачная база >> Национальные зарубежные олимпиады >> Польша >> 1997 >> 3 тур | Показать решения |