 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Польша >> 1999 >> 2 тур | Показать решения |
|
|
| Польская математическая олимпиада.. 1999. 2 тур |
|
|
Вещественнозначная функция f определена на отрезке [0,1] и удовлетворяет равенству f(1/n) = ( – 1)n при всех натуральных n. Докажите, что f нельзя представить в виде разности возрастающих функций.
Задача 2:Трехмерный уголок – куб 2 × 2 × 2, из которого вырезали угловой кубик. Докажите, что куб 2n × 2n × 2n с вырезанным единичным кубиком можно разрезать на трехмерные уголки.
Задача 3:На сторонах AB и CD вписанного четырехугольника ABCD выбрали точки E и F соответственно, притом AE:EB = CF:FD. На отрезке EF взяли точку P такую, что EP:PF = AB:CD. Докажите, что отношение площадей треугольников APD и BPC не зависит от выбора точек E и F.
Задача 4:
Внутри треугольника ABC взяли точку P такую, что ∠ PAB = ∠ PCA и ∠ PAC = ∠ PBA. Докажите, что если точка P не совпадает с центром описанной окружности O, то угол APO – прямой.
Задача 5:
Найдите количество перестановок σ множества из 5 элементов,
удовлетворяющих равенству 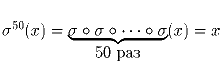
Целые числа a1,a2, … ,an удовлетворяют равенствам a1 + 2ia2 + 3ia3 + … + nian = 0 для всех i = 1,2, … ,k – 1 (k ≥ 2). Докажите, что a1 + 2ka2 + 3ka3 + … + nkan делится на k!.
| Задачная база >> Национальные зарубежные олимпиады >> Польша >> 1999 >> 2 тур | Показать решения |