 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Putnam >> 1996 >> A | Убрать решения |
|
|
| Американская студенческая олимпиада. 1996. A |
|
|
Найти наименьшее A, при котором для любых двух квадратов общей площади 1 найдется такой прямоугольник площади A, в котором можно разместить без наложения указанные квадраты. Можно считать, что стороны квадратов параллельны сторонам прямоугольника.
Решение: Пусть площади квадратов x и 1 – x. Можно считать, что x ≥ 1/2. Прямоугольник наименьшей площади, содержащий оба квадрата, имеет вид:
Его площадь  Задача сводится к нахождению наибольшего значения функции S(x) на
промежутке [1/2,1].
Задача сводится к нахождению наибольшего значения функции S(x) на
промежутке [1/2,1].
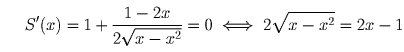
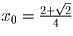 . Значение S(x0) удобно вычислить так:
. Значение S(x0) удобно вычислить так:
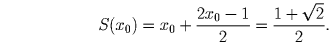
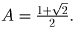
Задача 2:
Радиусы двух окружностей соответственно 1 и 3, расстояние между центрами окружностей – 10. Найти геометрическое место середин отрезков, соединяющих точки данных окружностей.
Решение:Введем на плоскости систему координат так, чтобы центры окружностей лежали на оси абсцисс симметрично относительно начала координат. Параметрические уравнения окружностей будут иметь вид: x1 = – 5 + cos t1, y1 = sin t1 и x2 = 5 + 3 cos t2, y2 = sin t2 соответственно. Для точки (x,y), являющейся серединой отрезка, соединяющего точки (x1,y1) и (x2,y2), имеем: (x,y) = ½( cos t1 + 3 cos t2, sin t1 + 3 sin t2). Если зафиксировать t2, то с изменением t1 от 0 до 2 π точка (x,y) будет описывать окружность радиуса 1/2. При изменении t2 от 0 до 2 π центр указанной окружности (3/2 cos t2,3/2 sin t2) в свою очередь будет двигаться по окружности радиуса 3/2 с центром в начале координат; окружность радиуса 1/2 будет при этом «заметать» кольцо с внутренним радиусом 3/2 – 1/2 = 1 и внешним радиусом 3/2 + 1/2 = 2. Ответ. Геометрическое место точек представляет собой кольцо, центр которого есть середина отрезка, соединяющего центры окружностей, а внутренний и внешний радиусы равны соответственно 1 и 2.
Задача 3:
В школе работает 6 кружков. Каждый из 20 учеников класса может посещать любое количество кружков – от 0 до 6. Верно ли, что обязательно найдутся такие 5 учеников и такие 2 кружка, что все пятеро либо посещают оба кружка, либо не посещают ни один из этих двух кружков?
Решение: Ответ.Нет. Заметим, что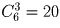 . Пусть каждый ученик посещает
ровно три кружка, причем у каждого набор кружков отличен от других. (В силу
сделанного замечания это возможно.) Тогда и наборы непосещаемых кружков также
будут разными у разных учеников. Если бы некоторые 5 человек посещали
одновременно какие-нибудь два кружка, тогда из оставшихся четырех кружков по
крайней мере один пришлось бы посещать одновременно двум (принцип Дирихле),
что приводит к противоречию. Последняя фраза останется справедливой, если в
ней перед словами «посещали», «посещать» поставить частицу «не».
. Пусть каждый ученик посещает
ровно три кружка, причем у каждого набор кружков отличен от других. (В силу
сделанного замечания это возможно.) Тогда и наборы непосещаемых кружков также
будут разными у разных учеников. Если бы некоторые 5 человек посещали
одновременно какие-нибудь два кружка, тогда из оставшихся четырех кружков по
крайней мере один пришлось бы посещать одновременно двум (принцип Дирихле),
что приводит к противоречию. Последняя фраза останется справедливой, если в
ней перед словами «посещали», «посещать» поставить частицу «не».Задача 4:
Пусть S – множество упорядоченных троек (a,b,c) различных элементов конечного множества A. Выполняются следующие условия:
 ;
;
 ;
;
 .
.
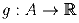 , что из
двойного неравенства g(a) < g(b) < g(c) следует: (a,b,c) ∈ S.
Решение:
, что из
двойного неравенства g(a) < g(b) < g(c) следует: (a,b,c) ∈ S.
Решение: Пусть в множестве A n элементов. Из 2) следует, что ровно
половина всех упорядоченных троек (различных) элементов A входит в S.
Зафиксируем некоторый элемент w ∈ A и на множестве 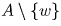 введем отношение ρ :
введем отношение ρ : 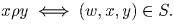 Легко видеть, что оно
антисимметрично: если x ρ y, то неверно, что y ρ x. Докажем, что данное
отношение транзитивно. Пусть x ρ y и y ρ z. Тогда (w,x,y) ∈ S и
(w,y,z) ∈ S. В силу 1) и (y,z,w) ∈ S. В силу 2) S принадлежат и тройки
(x,y,z),(z,w,x). Опять применяя 1), получим, что (w,x,z) ∈ S, т.е. x ρ z, что и требовалось доказать. Обозначим через ki количество элементов x
из множества
Легко видеть, что оно
антисимметрично: если x ρ y, то неверно, что y ρ x. Докажем, что данное
отношение транзитивно. Пусть x ρ y и y ρ z. Тогда (w,x,y) ∈ S и
(w,y,z) ∈ S. В силу 1) и (y,z,w) ∈ S. В силу 2) S принадлежат и тройки
(x,y,z),(z,w,x). Опять применяя 1), получим, что (w,x,z) ∈ S, т.е. x ρ z, что и требовалось доказать. Обозначим через ki количество элементов x
из множества 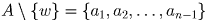 таких, что ai ρ x. Если ai ρ aj, то из-за транзитивности и антисимметричности
ki > kj. (Действительно, с одной стороны,
таких, что ai ρ x. Если ai ρ aj, то из-за транзитивности и антисимметричности
ki > kj. (Действительно, с одной стороны, 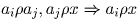 — этим обеспечивается нестрогое неравенство; с другой
стороны неверно,
что aj ρ ai). Нетрудно видеть, что верно и обратное: если ki > kj, то
ai ρ aj (по закону контрапозиции). Положим g(ai) = n – 1 – ki, g(w) = n.
Покажем, что функция g обладает требуемыми свойствами. Если g(a) < g(b), то
a ρ b, или (w,a,b) ∈ S. Если c = w, то из того, что(c,a,b) ∈ S
в силу 2)
следует: (a,b,c) ∈ S. Если же c ≠ w, то из g(b) < g(c) получаем:
(w,b,c) ∈ S, стало быть, (b,c,w) ∈ S. Поскольку при этом и (w,a,b) ∈ S, то в силу 3) (a,b,c) ∈ S.
— этим обеспечивается нестрогое неравенство; с другой
стороны неверно,
что aj ρ ai). Нетрудно видеть, что верно и обратное: если ki > kj, то
ai ρ aj (по закону контрапозиции). Положим g(ai) = n – 1 – ki, g(w) = n.
Покажем, что функция g обладает требуемыми свойствами. Если g(a) < g(b), то
a ρ b, или (w,a,b) ∈ S. Если c = w, то из того, что(c,a,b) ∈ S
в силу 2)
следует: (a,b,c) ∈ S. Если же c ≠ w, то из g(b) < g(c) получаем:
(w,b,c) ∈ S, стало быть, (b,c,w) ∈ S. Поскольку при этом и (w,a,b) ∈ S, то в силу 3) (a,b,c) ∈ S.
Задача 5:
Пусть p – простое число, большее 3, k = [2p/3]. Доказать, что сумма
биномиальных коэффициентов 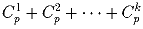 делится на
p².
делится на
p².
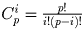 — целое число; числитель дроби кратен p, а
знаменатель — нет (так как p — простое число)). Доказываемое утверждение
равносильно делимости на p суммы
— целое число; числитель дроби кратен p, а
знаменатель — нет (так как p — простое число)). Доказываемое утверждение
равносильно делимости на p суммы  .
Проведем сравнение по модулю p:
.
Проведем сравнение по модулю p:
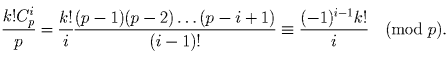
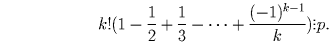
 Имеем:
Имеем:

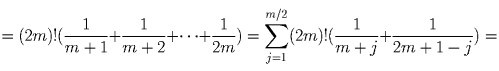
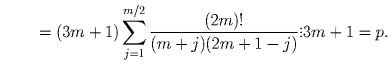
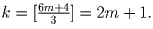 Имеем:
Имеем:
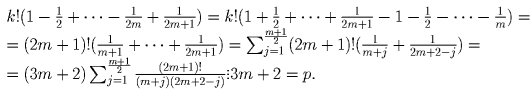
Задача 6:
Пусть 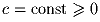 . Опишите множество всех непрерывных функций
. Опишите множество всех непрерывных функций
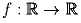 таких, что
таких, что 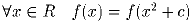 .
.
Решение: По условию f – четная функция и f(0) = f(c). В дальнейшем будем считать, что все рассматриваемые переменные, константы, последовательности являются неотрицательными. Рассмотрим последовательность x0 = x,
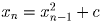 (n ∈ N),
во всех
точках которой функция f должна принимать одно и то же значение. Если
эта последовательность имеет конечный предел a, то для определения a
имеем (с помощью
перехода к пределу в рекуррентном соотношении) уравнение: a = a² + c, у
которого нет
решений при c > ¼; единственное решение a = ½ при
c = ¼ и два решения
(n ∈ N),
во всех
точках которой функция f должна принимать одно и то же значение. Если
эта последовательность имеет конечный предел a, то для определения a
имеем (с помощью
перехода к пределу в рекуррентном соотношении) уравнение: a = a² + c, у
которого нет
решений при c > ¼; единственное решение a = ½ при
c = ¼ и два решения 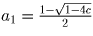 и
и
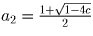 при 0 < c < ¼.
В зависимости от значений c рассмотрим различные случаи.
при 0 < c < ¼.
В зависимости от значений c рассмотрим различные случаи.
 .
Пусть x0 = 0, тогда x1 = c, а отображение x → x² + c переводит отрезок
[xi – 1,xi] в отрезок [xi,xi + 1]. На промежутке [0,c] зададим
функцию f произвольным образом, лишь бы функция была непрерывна на нем и
f(0) = f(c). Тогда соотношением f(x) = f(x² + c) функция последовательно
задается на отрезках [x0,x1],[x1,x2], … – на всей положительной
полуоси, а в силу четности и на всей числовой прямой. Нетрудно видеть, что
построенная функция удовлетворяет условию задачи; в то же время произвольная
функция, удовлетворяющая условию задачи, имеет указанный вид.
.
Пусть x0 = 0, тогда x1 = c, а отображение x → x² + c переводит отрезок
[xi – 1,xi] в отрезок [xi,xi + 1]. На промежутке [0,c] зададим
функцию f произвольным образом, лишь бы функция была непрерывна на нем и
f(0) = f(c). Тогда соотношением f(x) = f(x² + c) функция последовательно
задается на отрезках [x0,x1],[x1,x2], … – на всей положительной
полуоси, а в силу четности и на всей числовой прямой. Нетрудно видеть, что
построенная функция удовлетворяет условию задачи; в то же время произвольная
функция, удовлетворяющая условию задачи, имеет указанный вид.
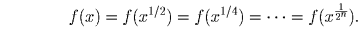
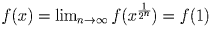 .
Привлекая свойство четности, получаем: f(x) = const.
.
Привлекая свойство четности, получаем: f(x) = const.
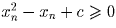 ,
откуда
,
откуда  ; кроме того:
; кроме того:  . Таким образом, если x0 = x ≤ a1, то
последовательность (xn) возрастает, ограничена сверху числом a1 и имеет
его своим пределом (по теореме Вейерштрасса предел существует; с другой
стороны он не равен a2, так как
. Таким образом, если x0 = x ≤ a1, то
последовательность (xn) возрастает, ограничена сверху числом a1 и имеет
его своим пределом (по теореме Вейерштрасса предел существует; с другой
стороны он не равен a2, так как  .
Итак, для
x0 = x ≤ a1 (переходя к пределу по n в тождестве
f(x) = f(x0) = f(xn) и используя непрерывность f) получаем: f(x) = f(a1).
.
Итак, для
x0 = x ≤ a1 (переходя к пределу по n в тождестве
f(x) = f(x0) = f(xn) и используя непрерывность f) получаем: f(x) = f(a1).
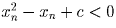 ,
откуда
,
откуда 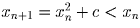 ; кроме того:
; кроме того: 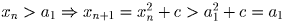 . Таким образом, если
a1 < x0 < a2,
то последовательность (xn) убывает, ограничена снизу
числом a1 и имеет его своим пределом (предел
существует и он не равен a2, так как ∀ n xn ≤ x0 < a2). Итак, для a1 < x0 = x < a2
с помощью предельного перехода
вновь получаем: f(x) = f(a1).
. Таким образом, если
a1 < x0 < a2,
то последовательность (xn) убывает, ограничена снизу
числом a1 и имеет его своим пределом (предел
существует и он не равен a2, так как ∀ n xn ≤ x0 < a2). Итак, для a1 < x0 = x < a2
с помощью предельного перехода
вновь получаем: f(x) = f(a1).
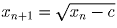 (для функции f из условия задачи ∀ n ∈ N f(xn) = f(x0).
Имеем: при
(для функции f из условия задачи ∀ n ∈ N f(xn) = f(x0).
Имеем: при 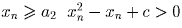 ,
откуда
,
откуда 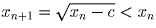 ; кроме того:
; кроме того:  т.е.
т.е.
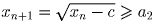 .
Таким образом, если x0 ≥ a2,
то последовательность (xn) убывает, ограничена снизу
числом a2 и имеет его своим пределом (предел
существует и не равен a1, так как
.
Таким образом, если x0 ≥ a2,
то последовательность (xn) убывает, ограничена снизу
числом a2 и имеет его своим пределом (предел
существует и не равен a1, так как 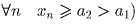 .
Итак, для x = x0 ≥ a2
(переходя к пределу по n в тождестве f(x) = f(x0) = f(xn)
) получаем: f(x) = f(a2).
.
Итак, для x = x0 ≥ a2
(переходя к пределу по n в тождестве f(x) = f(x0) = f(xn)
) получаем: f(x) = f(a2).
| Задачная база >> Национальные зарубежные олимпиады >> Putnam >> 1996 >> A | Убрать решения |