 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Putnam >> 1996 >> B | Показать решения |
|
|
| Американская студенческая олимпиада. 1996. B |
|
|
Назовем множество эгоцентричным (или э-множеством), если оно содержит свою мощность (число элементов). (Например, 2,3,3,5,8 – э-множества, а 3,5,2,5,8 не являются таковыми). Найти число подмножеств множества 1,2, … ,n, являющихся минимальными э-множествами, т.е. такими эгоцентричными множествами, чьи собственные подмножества – не э-множества. (Пример. 2,3 – минимальное э-множество в отличие от 1,2).
Задача 2:Доказать, что для любого натурального числа n

Задача 3:
Пусть x1,x2, … ,xn = 1,2, … ,n. Найти как функцию от n (n > 2) наибольшее значение выражения x1x2 + x2x3 + … + xn – 1xn + xnx1.
Задача 4:Для произвольной квадратной матрица A определим sin A с помощью степенного ряда:
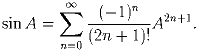
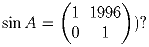
Для строки S, состоящей из единиц и нулей, обозначим через Δ (S) разность числа единиц и нулей. Например, Δ (1001001) = – 1. Назовем строку S сбалансированной, если для любой подстроки T (последовательных символов) S – 2 ≤ Δ (T) ≤ 2. Так, строка 1001001 не является сбалансированной, так как содержит подстроку 00100. Найти число сбалансированных строк длины n.
Задача 6:Пусть 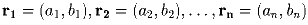 – радиус-векторы вершин выпуклого многоугольника,
внутри которого находится начало координат. Доказать, что существуют такие
положительные числа x и y, что
– радиус-векторы вершин выпуклого многоугольника,
внутри которого находится начало координат. Доказать, что существуют такие
положительные числа x и y, что
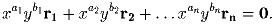
| Задачная база >> Национальные зарубежные олимпиады >> Putnam >> 1996 >> B | Показать решения |