 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Putnam >> 1996 >> B | Убрать решения |
|
|
| Американская студенческая олимпиада. 1996. B |
|
|
Назовем множество эгоцентричным (или э-множеством), если оно содержит свою мощность (число элементов). (Например, 2,3,3,5,8 – э-множества, а 3,5,2,5,8 не являются таковыми). Найти число подмножеств множества 1,2, … ,n, являющихся минимальными э-множествами, т.е. такими эгоцентричными множествами, чьи собственные подмножества – не э-множества. (Пример. 2,3 – минимальное э-множество в отличие от 1,2).
Решение: Обозначим число искомых подмножеств fn. Выпишем минимальные э-множества при n ≤ 6: 1,2,3,2,4,2,5,2,6,3,4,5,3,4,6,3,5,6. Прямой подсчет показывает: f1 = f2 = 1,f3 = 2,f4 = 3,f5 = 5,f6 = 8. Возникает предположение, что для для любого натурального n fn + 2 = fn + 1 + fn. Убедимся в этом.Разобьем все мэ-подмножества множества 1,2, … ,n + 2 на два класса: множеств, содержащих число n + 2, и множеств, не содержащих это число. Всякое множество из второго класса является мэ-подмножеством множества 1,2, … ,n + 1, поэтому во втором классе fn + 1 множеств.
Заметим, что в минимальном э-множестве, содержащем k элементов, не могут присутствовать числа меньше k (из-за минимальности), и так как множество – эгоцентрично, то число k – его элемент. Легко проверить, что верно и обратное: произвольное k-элементное множество с минимальным элементом k будет мэ-множеством.
Возьмем теперь произвольное множество из первого класса (пусть k – число его элементов; ясно, что k > 2), удалим в нем элемент n + 2, а все остальные элементы уменьшим на единицу. Получим k – 1-элементное множество с минимальным элементом k – 1 – это мэ-множество, причем максимальный элемент его не превосходит n. Установлено взаимно однозначное соответствие между множествами из первого класса и мэ-подмножествами множества 1,2, … ,n. Таким образом, первый класс содержит fn множеств. Соотношение fn + 2 = fn + 1 + fn доказано. Ответ. fn — n-е число Фибоначчи.
Замечание.
Из чисел 1,2, … ,n можно составить 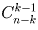 k-элементных
минимальных э-множеств (к числу k нужно добавить еще k – 1 больших k
чисел). Поэтому
k-элементных
минимальных э-множеств (к числу k нужно добавить еще k – 1 больших k
чисел). Поэтому
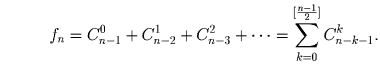
Задача 2:
Доказать, что для любого натурального числа n

Решение:
Логарифмированием получим неравенство, равносильное доказываемому:
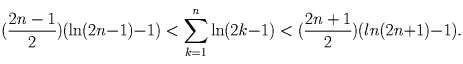
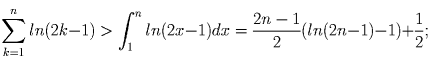
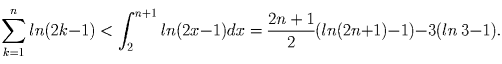
Задача 3:
Пусть x1,x2, … ,xn = 1,2, … ,n. Найти как функцию от n (n > 2) наибольшее значение выражения x1x2 + x2x3 + … + xn – 1xn + xnx1.
Решение: Можно считать, что числа x1,x2, … ,xn расположены по кругу и Sn – сумма попарных произведений соседних чисел.Докажем по индукции следующее утверждение: если Sn максимально, то число n стоит между числами n – 1 и n – 2. База индукции (n = 3) очевидна. Индукционный шаг. Пусть утверждение справедливо при n = k. Если число k + 1 вставляется между числами a и b, то сумма попарных произведений изменяется так: Δ k = Sk + 1 – Sk = (k + 1)(a + b) – ab. При фиксированном a Δ k = (k + 1)a + b(k + 1 – a) тем больше, чем больше b. Аналогично при фиксированном b Δ k увеличивается с ростом a. Поэтому Δ k ≤ (k + 1)(k + (k – 1)) – k(k – 1) = k² + 2k – 1. По предположению индукции если Sk максимально, то числа k и k – 1 стоят рядом. Если k + 1 вставить между этими числами, то получим максимальное значение Δ k = k² + 2k – 1, а заодно и Sk + 1 = Sk + Δ k, что и требовалось доказать.
Теперь легко найти Sn. S2 = 1 • 2 + 2 • 1 = 4. При n > 2
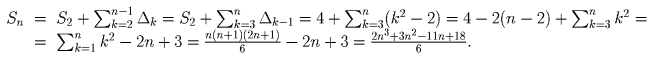
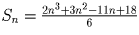 .
.Задача 4:
Для произвольной квадратной матрица A определим sin A с помощью степенного ряда:
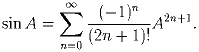
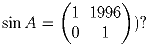
Определив с помощью степенного ряда cos A:
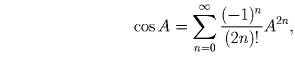
 ,
,
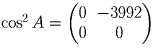 . Покажем, что не
существует такой матрицы
. Покажем, что не
существует такой матрицы 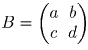 , что
, что
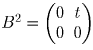 , где t ≠ 0. Действительно,
из системы уравнений
, где t ≠ 0. Действительно,
из системы уравнений
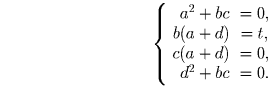
последовательно получаем: |a| = |d|, a + d ≠ 0, c = 0, d = 0, a = 0, приходя к противоречию. Таким образом, ответ к задаче будет отрицательным даже при замене числа 1996 на любое ненулевое число.
Задача 5:
Для строки S, состоящей из единиц и нулей, обозначим через Δ (S) разность числа единиц и нулей. Например, Δ (1001001) = – 1. Назовем строку S сбалансированной, если для любой подстроки T (последовательных символов) S – 2 ≤ Δ (T) ≤ 2. Так, строка 1001001 не является сбалансированной, так как содержит подстроку 00100. Найти число сбалансированных строк длины n.
Решение:Во-первых, из условия следует, что (сбалансированная) строка не содержит трех одинаковых подряд идущих символов. Во-вторых, если в строке встретилось подряд две единицы, то следующим повторяющимся символом может быть только ноль (и наоборот); при этом четность номеров позиций первых из пар повторяющихся символов будет одинаковой. Поэтому всякая сбалансированная строка полностью задается следующими условиями:
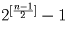 . Если учесть случай отсутствия пар
повторяющихся символов, то получим, что количество способов выбрать места для
расположения пар одинаковых символов равно
. Если учесть случай отсутствия пар
повторяющихся символов, то получим, что количество способов выбрать места для
расположения пар одинаковых символов равно
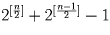 .
Ответ. Число сбалансированных строк длины n равно
.
Ответ. Число сбалансированных строк длины n равно
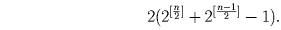
Задача 6:
Пусть 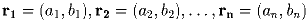 – радиус-векторы вершин выпуклого многоугольника,
внутри которого находится начало координат. Доказать, что существуют такие
положительные числа x и y, что
– радиус-векторы вершин выпуклого многоугольника,
внутри которого находится начало координат. Доказать, что существуют такие
положительные числа x и y, что
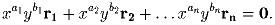
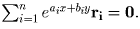 Нетрудно видеть, что последнее уравнение определяет
стационарную
точку функции
Нетрудно видеть, что последнее уравнение определяет
стационарную
точку функции 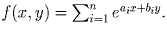 Заметим, что
Заметим, что
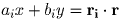 (скалярное произведение векторов), где
(скалярное произведение векторов), где
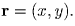 Пусть
Пусть 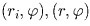 — полярные координаты точек (ai,bi)(i = 1, … ,n) и (x,y)
соответственно; ρ = min ri. Упорядочим векторы
— полярные координаты точек (ai,bi)(i = 1, … ,n) и (x,y)
соответственно; ρ = min ri. Упорядочим векторы 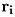 по возрастанию
полярного угла
по возрастанию
полярного угла 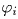 ; наибольший угол между соседними векторами обозначим
θ , ввиду условия задачи θ < π . Для любого вектора r
найдется такой вектор ri, что
; наибольший угол между соседними векторами обозначим
θ , ввиду условия задачи θ < π . Для любого вектора r
найдется такой вектор ri, что 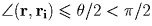 . Введя обозначение: p = ρ cos θ /2, cкалярное
произведение этих векторов оценим снизу:
. Введя обозначение: p = ρ cos θ /2, cкалярное
произведение этих векторов оценим снизу: 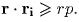 Отсюда вытекает равномерная оценка для функции
f:
Отсюда вытекает равномерная оценка для функции
f: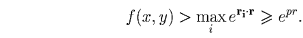
| Задачная база >> Национальные зарубежные олимпиады >> Putnam >> 1996 >> B | Убрать решения |