 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Putnam >> 1997 >> A | Показать решения |
|
|
| Американская студенческая олимпиада. 1997. A |
|
|
Прямоугольник HOMF имеет стороны HO = 11 и OM = 5. Для треугольника ABC точка H – точка пересечения высот, O – центр описанной окружности, M — середина BC, F – основание высоты, проведенной из вершины A. Найти длину BC.
Задача 2:За круглым столом сидят n игроков. Каждый из них первоначально имеет по одному рублю. Первый игрок передает рубль второму, после чего второй передает два рубля третьему. Затем третий игрок передает рубль четвертому, а четвертый два рубля пятому и т.д. Игроки поочередно передают рубль или два рубля следующему игроку, у которого еще есть деньги; игрок, лишившийся денег, выбывает из игры и покидает стол. Найти бесконечное множество таких n, при которых игра заканчивается тем, что у некоторого игрока оказываются все n рублей.
Задача 3: Вычислить
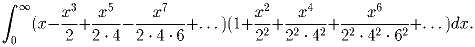
Задача 4:
Пусть G – группа с единичным элементом e; φ : G → G – функция такая, что φ (g1) φ (g2) φ (g3) = φ (h1) φ (h2) φ (h3), всякий раз, когда g1g2g3 = e = h1h2h3. Доказать, что существует такой элемент a ∈ G, что функция ψ (x) = a φ (x) есть гомоморфизм (т.е. ψ (xy) = ψ (x) ψ (y) для всех x,y ∈ G).
Задача 5:Для n = 10 определить, четно или нечетно число упорядоченных n-элементных наборов натуральных чисел (x1,x2, … ,xn) таких, что
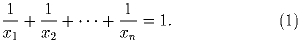
Пусть n – натуральное число, c – действительное число. Последовательность (xk) определяется соотношениями x0 = 0,x1 = 1 и
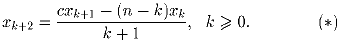
| Задачная база >> Национальные зарубежные олимпиады >> Putnam >> 1997 >> A | Показать решения |