 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Putnam >> 1997 >> B | Убрать решения |
|
|
| Американская студенческая олимпиада. 1997. B |
|
|
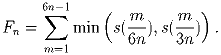
Обозначим
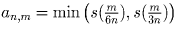 .
.
Пусть 1 ≤ m ≤ 2n. В этом случае
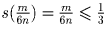 , в то же время
, в то же время
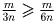 и
и 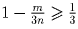 – значит,
– значит, 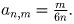
Если 2n < m ≤ 3n, выполняются
неравенства 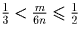 и
и
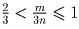 , из которых
следует, что
, из которых
следует, что 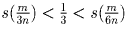 и
и
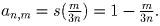
Заметим также, что
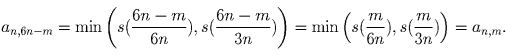
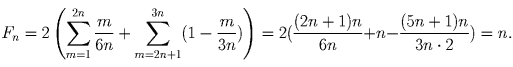
Пусть f — дважды дифференцируемая функция, для которой f″(x) + f(x) = – xg(x)f′(x), где g(x) ≥ 0 при всех x. Доказать, что функция f(x) ограничена.
Решение:Умножим обе части уравнения на 2f′(x), после чего проинтегрируем их на промежутке от 0 до t:
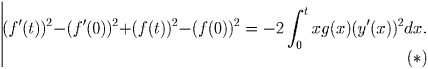
Задача 3: Для каждого натурального n запишем сумму
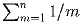 в виде α n/ β n, где α n и β n – взаимно простые числа.
Найти все n, при которых β n не делится на 5.
Решение:
Если натуральное число n представимо в виде n = 5ak, где a –
неотрицательное целое число, k – натуральное число, не кратное 5, будем
говорить, что n имеет ранг a. Условимся также, что рациональное
число
в виде α n/ β n, где α n и β n – взаимно простые числа.
Найти все n, при которых β n не делится на 5.
Решение:
Если натуральное число n представимо в виде n = 5ak, где a –
неотрицательное целое число, k – натуральное число, не кратное 5, будем
говорить, что n имеет ранг a. Условимся также, что рациональное
число 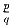 , где p и q – взаимно простые числа, имеет порядок a, если знаменатель q имеет ранг a. Задача, таким образом,
состоит в нахождении всех n, для которых число
, где p и q – взаимно простые числа, имеет порядок a, если знаменатель q имеет ранг a. Задача, таким образом,
состоит в нахождении всех n, для которых число 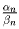 имеет нулевой порядок.
имеет нулевой порядок.1. Сумма рациональных чисел разного порядка имеет наибольший из этих порядков.
Действительно, пусть a > b, p1,p2,q1,q2 – числа, не делящиеся на 5;
тогда
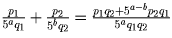 — числитель полученной дроби не делится на 5, а знаменатель имеет ранг a.
— числитель полученной дроби не делится на 5, а знаменатель имеет ранг a.
2. Проследим за тем, как меняется порядок при сложении величин, обратных последовательным числам одного ранга.
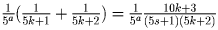 – порядок не меняется;
– порядок не меняется;
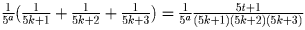 – порядок не меняется;
– порядок не меняется;
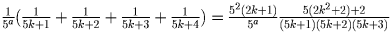 – порядок
уменьшается.
– порядок
уменьшается.
3. Решим задачу для n ≤ 124.
В силу 1o при переходе от 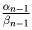 к
к
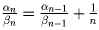 порядок
дроби может измениться лишь при n, кратном 5. Отметим, что
порядок
дроби может измениться лишь при n, кратном 5. Отметим, что
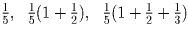 имеют порядок 1, а остальные
слагаемые суммы
имеют порядок 1, а остальные
слагаемые суммы 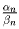 имеют нулевой порядок);
имеют нулевой порядок);
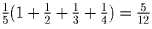 , а остальные
слагаемые вновь нулевого порядка);
, а остальные
слагаемые вновь нулевого порядка);
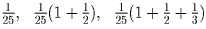 имеют порядок 2, а остальные
слагаемые суммы
имеют порядок 2, а остальные
слагаемые суммы 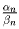 имеют меньший порядок);
имеют меньший порядок);
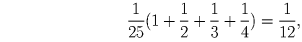
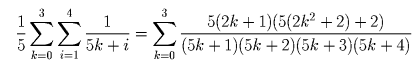
4. Пусть n ≥ 125, a – наибольший ранг чисел от 1 до
n, r • 5a
— наибольшее число такого ранга. Ясно, что a ≥ 3, а число r равно 1,
2, 3 или 4.
Соотношения из пункта 2o показывают, что при r < 4 число
 будет иметь порядок a. Пусть теперь r = 4. Тогда
сумма дробей порядка a имеет порядок a – 2:
будет иметь порядок a. Пусть теперь r = 4. Тогда
сумма дробей порядка a имеет порядок a – 2:
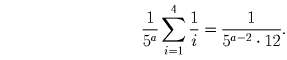
 имеет порядок a – 1 (в силу 1o);
будем поэтому считать, что имеет место второй случай.
имеет порядок a – 1 (в силу 1o);
будем поэтому считать, что имеет место второй случай.Пусть (5k + s)5a – 2 – наибольшее число ранга a – 2, не превосходящее n.
При этом s = 1,2,3 или 4.
Отметим, что сумма 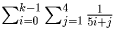 имеет порядок
меньше a – 2. Осталось найти порядок суммы
имеет порядок
меньше a – 2. Осталось найти порядок суммы 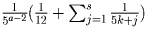 . С помощью соотношений из пункта 2o
непосредственно проверяется, что для любого s эта сумма имеет порядок a – 2.
. С помощью соотношений из пункта 2o
непосредственно проверяется, что для любого s эта сумма имеет порядок a – 2.
Итак, при n ≥ 125 дробь 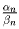 имеет ненулевой порядок.
имеет ненулевой порядок.
Ответ. β n не делится на 5 при только приn = 1, … ,4,20, … ,24,100, … ,104,120, … ,124.
Задача 4:
(1 + x + x²)m. Докажите, что для всех целых k ≥ 0
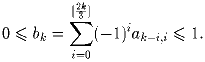
Полагая am,i = 0 при i < 0 и i > 2m, запишем очевидное
рекуррентное соотношение
am + 1,n = am,n + am,n – 1 + am,n – 2.
Заметим, что числа ak – i,i отличны от нуля лишь при
2(k – i) ≥ i, то есть когда 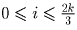 . Поэтому с
учетом принятого соглашения во всех последующих выкладках будем
считать, что индекс суммирования меняется от 0 до + ∞ .
. Поэтому с
учетом принятого соглашения во всех последующих выкладках будем
считать, что индекс суммирования меняется от 0 до + ∞ .
Получим рекуррентную формулу для последовательности bm: bm + 1 = ∑ i( – 1)iam + 1 – i,i = ∑ i( – 1)i(am – i,i + am – i,i – 1 + am – i,i – 2) = ∑ i( – 1)iam – i,i – ∑ j( – 1)ja(m – 1) – j,j + ∑ k( – 1)ka(m – 2) – k,k = bm – bm – 1 + bm + 2. Непосредственные вычисления дают: b0 = 1,b1 = 1,b2 = 0,b3 = 0,b4 = 1,b5 = 1,b6 = 0,b7 = 0,b8 = 1. С помощью найденного рекуррентного соотношения по индукции легко доказать, что ∀ m ≥ 0 bm + 4 = bm. Таким образом последовательность периодична и ее члены принимают только два значения: 0 и 1. Это доказывает утверждение задачи.
Задача 5:
Докажите, что для n ≥ 2
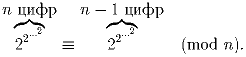
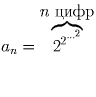 и
bn = an – an – 1. Докажем сначала, что в последовательности (bn)
каждый член (начиная с b3) делится на предыдущий (значит, и на все
предыдущие). Действительно,
и
bn = an – an – 1. Докажем сначала, что в последовательности (bn)
каждый член (начиная с b3) делится на предыдущий (значит, и на все
предыдущие). Действительно, 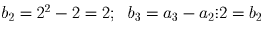 .
Предположим, что
.
Предположим, что 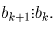 Тогда
Тогда
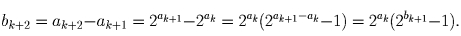
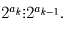 Так как (по предположению индукции)
Так как (по предположению индукции) 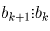 , имеем также
, имеем также
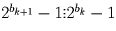 . Таким образом,
. Таким образом, 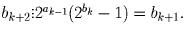
Перейдем к непосредственному доказательству утверждения задачи.
Оно также проводится методом математической индукции. База индукции
очевидна (b2 = 2). Пусть теперь для любого k < n выполняется
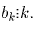
Представим число n в виде n = 2st, где t – нечетное
число. Легко проверить, что при n ≥ 3 имеет место неравенство
an – 2 > n. Отсюда 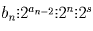 .
Теперь осталось доказать, что
.
Теперь осталось доказать, что 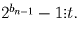
Применим теорему Эйлера. Заметим, что
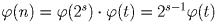 . Поэтому
. Поэтому
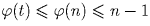 . Для любого k ≤ n – 1 имеем
. Для любого k ≤ n – 1 имеем
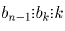 . В частности,
. В частности, 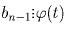 . Отсюда следует, что
. Отсюда следует, что 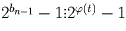 . В силу теоремы Эйлера
. В силу теоремы Эйлера 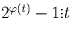 . Из последних двух соотношений и вытекает, что
. Из последних двух соотношений и вытекает, что 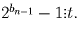 Таким образом,
Таким образом, 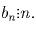
Решение: Возьмем на отрезке OH точку B, а на отрезке HG точку A так, чтобы HB = BA = AG. Введем систему координат так, как показано на рисунке.
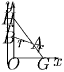
Пусть HB = r.
Тогда точки будут иметь следующие координаты: 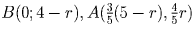 . Условие AB² = r² дает уравнение
. Условие AB² = r² дает уравнение
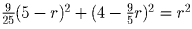 ,
один из корней которого r = 5 является посторонним (так как r < 4), а второй
равен
,
один из корней которого r = 5 является посторонним (так как r < 4), а второй
равен 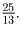
Легко проверить, что для точек O,G,H,A,B расстояние между любыми двумя
из них не меньше 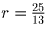 . Так как при любом разбиении треугольника
OGH на четыре части в одну из них попадет две из указанных пяти точек,
диаметр разбиения не меньше r.
. Так как при любом разбиении треугольника
OGH на четыре части в одну из них попадет две из указанных пяти точек,
диаметр разбиения не меньше r.
Приведем пример разбиения диаметра r. Пусть E ∈ HG,EH = r;\ K ∈ OG,KG = r; D ∈ OH,KD = r; точка C находится на расстоянии r от точек O и G. Тогда треугольник HBE, четырехугольники OKCD, KGAC и пятиугольник CAEBD образуют требуемое разбиение.
Для того, чтобы доказать это, заметим, что диаметр многоугольника есть
расстояние между некоторыми его вершинами. Несложно определить координаты
точек:
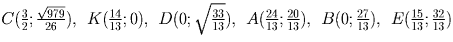 ,
а затем проверить, что диаметр каждой из
четырех частей разбиения равен
,
а затем проверить, что диаметр каждой из
четырех частей разбиения равен 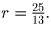
Ответ. Наименьший диаметр разбиения на четыре части
треугольника со сторонами длиной
3, 4, 5
равен 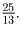
| Задачная база >> Национальные зарубежные олимпиады >> Putnam >> 1997 >> B | Убрать решения |