Задача 1:

Докажите, что не существует функции 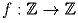такой, что f(f(x)) = x + 1 для любого .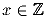

Задача 2:

Заполните следующую таблицу натуральными числами так, чтобы числа в каждой строке и каждом столбце образовывали бы арифметическую прогрессию:

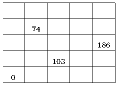
Задача 3:

Докажите, что числа

являются точными квадратами (каждое число записывается n четверками, n – 1 восьмеркой и девяткой).

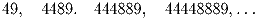
Задача 4:

Диагонали вписанного четырехугольника ABCD пересекаются в точке S. Q – середина стороны AB, P и R – основания перпендикуляров, опущенных из точки S на стороны AD и BC. Докажите, что PQ = QR.