 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Тайвань >> 1995 | Показать решения |
|
|
| Тайваньская математическая олимпиада.. 1995 |
|
|
P(x) = a0 + a1x + a2x² + … + anxn – многочлен с комплексными коэффициентами. α 1, α 2,…, α n – корни P(x), притом | α 1| > 1, | α 2| > 1,…, | α j| > 1 и | α j + 1| ≤ 1,…, | α n| ≤ 1. Докажите, что
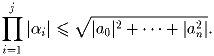
Задача 2:
Из последовательности из 8 целых чисел x1, … ,x8 разрешается получить послежовательность |x2 – x1|, |x3 – x2|,…, |x8 – x7|, |x1 – x8|. Найдите все целочисленные последовательности из которых за конечное число таких операций можно получить 8 равных чисел.
Задача 3:
В компании из n человек каждый знаком ровно с 8 другими, притом, у любых двух знакомых есть 4 общих знакомых, а у любых двух не знакомых – 2 общих знакомых. Найдите все возможные значения n.
Задача 4:
Докажите, что для любых n различных целых чисел m1, m2,…, mn существует неприводимый многочлен n-й степени с целыми коэффициентами f(x) такой, что f(mi) = – 1.
Задача 5:
Из точки P на описанной около треугольника ABC окружности опустили перпендикуляры на прямые, содержащие стороны треугольника. Основания перпендикуляров лежат на одной прямой. Докажите, что эта прямая проходит через середину отрезка PH, где H – ортоцентр треугольника ABC.
Задача 6:
a, b, c, d – целые числа, притом (a,b) = 1 и (c,d) = 1. Пусть ad – bc = k > 0. Докажите, что существует ровно k различных пар вещественных чисел (x1,x2) таких, что 0 ≤ x1,x2 < 1, а числа ax1 + bx2 и cx1 + dx2 – целые.
В
| Задачная база >> Национальные зарубежные олимпиады >> Тайвань >> 1995 | Показать решения |