 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> США >> 1993 | Показать решения |
|
|
| Математическая олимпиада США. 1993 |
|
|
Для каждого натурального n ≥ 2 определите (с доказательством) какое из двух вещественных чисел a или b больше, если
an = a + 1, а b2n = b + 3a.
Задача 2:ABCD – выпуклый четырехугольник, диагонали которого перпендикулярны и пересекаются в точке E. Докажите, что точки симметричные E относительно прямых AB,BC,CD,DA лежат на одной окружности.
Задача 3:
Рассмотрим все вещественнозначные функции f, определенные на отрезке [0,1], удовлетворяющие следующим трем свойствам:
1) f(x) ≥ 0 для всех x из [0,1];
2) f(1) = 1;
3) f(x) + f(y) ≤ f(x + y) для любых x,y,x + y из отрезка [0,1].
Найдите такую наименьшую константу c, что f(x) ≤ cx для любой функции f удовлетворяющей условиям (1) – (3) и для любого x из отрезка [0,1].
Задача 4:a и b – два нечетных натуральных числа. Последовательность fn определяется следующим способом: f1 = a, f2 = b. При n ≥ 3 fn определяется как наибольший нечетный делитель fn – 1 + fn – 2. Докажите, что для достаточно больших n значение fn постоянно, и найдите это значение как функцию от a и b.
Задача 5:
a0,a1,a2, … – последовательность положительных
вещественных чисел такая, что для любого i 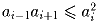 (такие последовательности называются логарифмически вогнутыми). Докажите,
что при n > 1
(такие последовательности называются логарифмически вогнутыми). Докажите,
что при n > 1
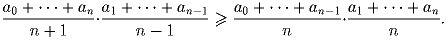
| Задачная база >> Национальные зарубежные олимпиады >> США >> 1993 | Показать решения |