 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> США >> 1999 | Показать решения |
|
|
| Математическая олимпиада США. 1999 |
|
|
На доске n × n расставлены шашки, притом каждая пустая клетка граничит (по стороне) с клеткой, в которой стоит шашка, и любые две шашки соединены путем (последовательностью клеток, граничащих по стороне), на каждой клетке которого стоит шашка. Докажите, что количество шашек, стоящих на доске не меньше (n² – 2)/3.
Задача 2:ABCD – вписанный четырехугольник. Докажите, что |AB – CD| + |AD – BC| ≥ 2|AC – BD|.
Задача 3:p – простое число больше 2 и целые числа a,b,c,d не делятся на p, притом для любого не делящегося на p целого числа r ra/p + rb/p + rc/p + rd/p = 2. Докажите, что по среди сумм a + b, a + c, a + d, b + c, b + d, c + d по крайней мере две делятся на p.
Задача 4:
a1,a2, … ,an (n > 3) – вещественные числа, притом
a1 + a2 + • s + an ≥ n и
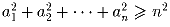 .
Докажите, что max (a1,a2, … ,an) ≥ 2.
.
Докажите, что max (a1,a2, … ,an) ≥ 2.
Двое играют в следующую игру: они по очереди записывают в клетках полоски 1 × 2000 буквы S или O Выигрывает тот игрок, после хода которого на доске будет записано слово SOS (в соседних клетках). Если к концу игры на доске не будет записано слова SOS, игра оканчивается вничью. Докажите, что второй игрок имеет выигрышную стратегию.
Задача 6:
ABCD – равнобочная трапеция с основаниями AB и CD. Окружность, вписанная в треугольник BCD касаетс CD в точке E. F – точка на биссектрисе угла DAC такая, что EF ⊥ CD. Окружность, описанная вокруг треугольника ACF пересекает CD в точках C и G. Докажите, что треугольник AFG равнобедренный.
| Задачная база >> Национальные зарубежные олимпиады >> США >> 1999 | Показать решения |