 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Югославия >> Югославский отбор на IMO >> 1995 | Показать решения |
|
|
| Национальные зарубежные олимпиады. Югославия. Югославский отбор на IMO. 1995 |
|
|
Найдите все тройки положительных рациональных чисел (x,y,z) с
x ≤ y ≤ z для которых числа xyz, x + y + z и 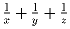 –
целые.
–
целые.
В двоичной записи числа n ровно 1995 единиц. Докажите, что n! делится на 2n – 1995.
Задача 3:
В пирамиде SABCD с основанием ABCD все ребра равны между собой. На ребрах BC и AS выбрали точки M и N соответственно так, что прямая MN перпендикулярна AD и BC. Найдите BM/MC и SN/NA.
| Задачная база >> Национальные зарубежные олимпиады >> Югославия >> Югославский отбор на IMO >> 1995 | Показать решения |