 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1980 >> Районный тур >> 9 класс ФМШ | Показать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада. 1980. Районный тур. 9 класс ФМШ |
|
|
Задача 2:
Задача 3:
Задача 4: p и q – простые числа. Найдите их, если известно, что уравнение x4 – px³ + q = 0 имеет целый корень.
Задача 5: Из точки A вне окружности радиуса R проведены к ней две касательные AB и AC, где B и C – точки касания. Пусть длина отрезка BC равна a. Доказать, что
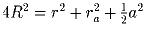 ,
где r –
радиус вписанной в треугольник ABC окружности, ra – радиус
вневписанной окружности.
,
где r –
радиус вписанной в треугольник ABC окружности, ra – радиус
вневписанной окружности.
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1980 >> Районный тур >> 9 класс ФМШ | Показать решения |