Задача 1:
Доказать, что положительный корень уравнения
x(x + 1)(x + 2) … (x + 1980)(x + 1981) = 1
меньше, чем
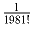
.
Задача 2:
Задача 3:
Найти все такие простые числа a и b, что a
b + b
a – тоже простое.
Задача 4:
Назовем сечение, проведенное в четырехугольной призме через
средние линии противоположных оснований параллельно боковым
ребрам, серединным сечением. Доказать, что для того, чтобы
диагональные сечения, проведенные через боковые ребра, были
взаимно перпендикулярны, необходимо и достаточно, чтобы
серединные сечения были равновелики.
Задача 5:
Пусть 0 < x < π /6. Доказать, что при всех натуральных n
sin x + + tg ²x + sin ³x + tg
4x + … + sin
2n – 1x + tg
2nx < 1,4.


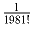 .
.