Задача 1:
Найти длины ребер прямоугольного параллелепипеда с квадратным
основанием, если они выражаются натуральными числами и площадь
поверхности параллелепипеда численно равна его периметру.
Задача 2:
Задача 3:
ABCD – выпуклый четырехугольник, ∠ BAC = ∠ CBD,
∠ ACD = ∠ BDA.
Докажите, что AC² = BC² + AD²
Задача 4:
Докажите, что при всех a,b,c > 0 выполнено неравенство
2
a + b + 2
b + c + 2
c + a < 2
a + b + c + 1 + 1.
Задача 5:
К каждой ветви гиперболы
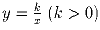
проведено по
касательной и точки пересечения касательных с осями координат
соединены отрезками. Доказать, что треугольники, отсеченные во
второй и четвертой четвертях, подобны.


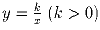 проведено по
касательной и точки пересечения касательных с осями координат
соединены отрезками. Доказать, что треугольники, отсеченные во
второй и четвертой четвертях, подобны.
проведено по
касательной и точки пересечения касательных с осями координат
соединены отрезками. Доказать, что треугольники, отсеченные во
второй и четвертой четвертях, подобны.