 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1981 >> Районный тур >> 9 класс ФМШ | Убрать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада. 1981. Районный тур. 9 класс ФМШ |
|
|
Решение: Пусть a – сторона основания, b – высота. Имеем: 4b + 8a = 2a² + 4ab, где a и b – натуральные числа. Заметим, что 4ab ≥ 4b всегда,а 2a² > 8a при любом a > 4. Значит, чтобы равенство было выполнено, в a должно быть не больше четырёх. Заметив, что a, кроме того, должно быть чётно, получаем единственный ответ: a = b = 2. Задача 2:
Задача 3: ABCD – выпуклый четырехугольник, ∠ BAC = ∠ CBD, ∠ ACD = ∠ BDA. Докажите, что AC² = BC² + AD²
Решение: Заметим, что треугольник ABC подобен треугольнику BOC, а треугольник AOD подобен треугольнику ADC (O – точка пересечения диагоналей). Значит
 и
и
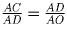 . Отсюда BC² + AD² = AC • OC + AC • AO = AC².
. Отсюда BC² + AD² = AC • OC + AC • AO = AC².Задача 4: Докажите, что при всех a,b,c > 0 выполнено неравенство 2a + b + 2b + c + 2c + a < 2a + b + c + 1 + 1.
Решение: Пусть 2a = A, 2b = B, 2c = C (A,B,C > 1). Перепишем доказываемое неравенство в виде 2ABC + 1 – AB – AC – BC > 0. Заметим, что
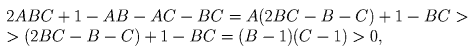
Задача 5: К каждой ветви гиперболы
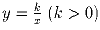 проведено по
касательной и точки пересечения касательных с осями координат
соединены отрезками. Доказать, что треугольники, отсеченные во
второй и четвертой четвертях, подобны.
проведено по
касательной и точки пересечения касательных с осями координат
соединены отрезками. Доказать, что треугольники, отсеченные во
второй и четвертой четвертях, подобны.Решение:
Найдём уравнение касательной к гиперболе в точке  . Уравнение прямой, проходящей через эту точку, имеет вид
. Уравнение прямой, проходящей через эту точку, имеет вид 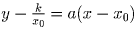 . Чтобы эта прямая была касательной,
необходимо, чтобы система
. Чтобы эта прямая была касательной,
необходимо, чтобы система

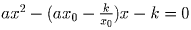 с дискриминантом
с дискриминантом
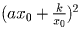 , откуда следует, что система имеет
единственное решение при
, откуда следует, что система имеет
единственное решение при
 . Таким образом уравнение касательной
(Знакомые с понятием производной могут найти уравнение
касательной гораздо быстрее) к
гиперболе
. Таким образом уравнение касательной
(Знакомые с понятием производной могут найти уравнение
касательной гораздо быстрее) к
гиперболе 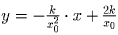 .
Эта касательная пересекает оси
координат в точках
.
Эта касательная пересекает оси
координат в точках  и (2x0;0).
Тогда произведение длин отрезков, отсекаемых на осях, равно
и (2x0;0).
Тогда произведение длин отрезков, отсекаемых на осях, равно
 . Мы видим, что это
произведение не зависит от выбора точки x0, а значит одинаково для
всех касательных. Из этого и следует требуемое подобие.
. Мы видим, что это
произведение не зависит от выбора точки x0, а значит одинаково для
всех касательных. Из этого и следует требуемое подобие.
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1981 >> Районный тур >> 9 класс ФМШ | Убрать решения |