 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1982 >> Районный тур >> 10 класс | Показать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада. 1982. Районный тур. 10 класс |
|
|
Задача 2: Доказать, что параболы y = a1x² и y = a2x² подобны.
Задача 3: Микрокалькулятор "Чебурашка" выполняет 4 арифметических действия и нахождение тангенса. Можно ли, пользуясь им, вычислить
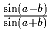 ?
?Задача 4: Длина высоты прямоугольного параллелепипеда ABCDA1B1C1D1 равна сумме длин двух смежных сторон основания. Доказать, что разность расстояний от точки M – проекции вершины B на диагональ основания AC – до вершин B1 и B равна длине диагонали основания.
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1982 >> Районный тур >> 10 класс | Показать решения |