 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1982 >> Районный тур >> 10 класс ФМШ | Убрать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада. 1982. Районный тур. 10 класс ФМШ |
|
|
Решение: Аналогично задаче 82.27. Ответ: x = y = z = 1982 + a.
Задача 2:
Задача 3: Пусть
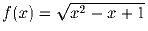 . Докажите, что уравнение
f(f(f(x))) = x имеет единственное решение x = 1.
. Докажите, что уравнение
f(f(f(x))) = x имеет единственное решение x = 1.Решение: При x > 1 выполнено неравенство 1 < x² – x + 1 < x² и, следовательно, 1 < f(x) < x, откуда f(f(f(x))) < x. При 0 < x < 1 выполнено нераенство x² < x² – x + 1 < 1 и, следовательно, x < f(x) < 1, откуда f(f(f(x))) > x. При x < 0 верно, что x² – x + 1 > 1 и f(f(f(x))) > x. x = 0 не удовлетворяет нашему уравнению, значит единственное решение x = 1.
Задача 4:
Задача 5: – 1 < x < 1 и 0 < p < 1. Докажите, что
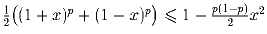 .
.Решение: Рассмотрим функцию f(x) = (1 + x)p + (1 – x)p – 2 + p(1 – p)x². Вычислим ее первую производную: f′(x) = p(1 + x)p – 1 – p(1 – x)p – 1 + 2p(1 – p)x, а затем вторую:
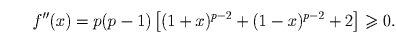
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1982 >> Районный тур >> 10 класс ФМШ | Убрать решения |