Задача 1:
Имеет ли вещественное решение уравнение
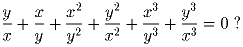
Задача 2:
Доказать, что касательные, проведенные к параболе y = ½x² из
точки

, взаимно перпендикулярны.
Задача 3:
В конечной возрастающей арифметической прогрессии сумма двух
каких-то последовательных членов, среди которых нет первого,
равна члену, следующему за ними. Найти прогрессию, если сумма её
членов равна 11d (d – разность прогрессии).
Задача 4:
ABCD – вписанный в окружность четырехугольник, причем
известно, что диагональ AC – биссектриса угла DAB. Докажите, что
AC • BD = AD • DC + AB • BC.
Задача 5:
Найдите все такие натуральные числа x,y,z, что равенство
x
n + y
n = z
n + 1
имеет место при любом натуральном n.


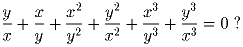
 , взаимно перпендикулярны.
, взаимно перпендикулярны.