 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1982 >> Районный тур >> 9 класс ФМШ | Показать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада. 1982. Районный тур. 9 класс ФМШ |
|
|
Задача 2: Найти такое наименьшее натуральное число k, что композиция k поворотов на 19 является поворотом на 10 .
Задача 3:
Задача 4: ABCD – вписанный в окружность четырехугольник. A1,B1,C1,D1 – середины дуг AB, AC, CD, DA соответственно. Докажите, что
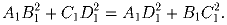
Задача 5: Найдите все такие натуральные числа x, y, z, что равенство 989xn + 993yn = zn + 1 верно при всех натуральных n.
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1982 >> Районный тур >> 9 класс ФМШ | Показать решения |