 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1983 >> Районный тур >> 10 класс ФМШ | Убрать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада. 1983. Районный тур. 10 класс ФМШ |
|
|
Задача 2:
Задача 3:
Задача 4: Рассмотрим всевозможные параболы y = x² + ax + b², пересекающие оси координат в трех разных точках. Для каждой такой параболы через эти три точки проведем окружность. Докажите, что все окружности имеют общую точку.
Решение: Точки пересечения параболы с осями имеют координаты: (x1;0), (x2;0), (0;b²), где x1 и x2 – корни квадратного трехчлена ax² + x + b². Обозначим их A, B, C соответственно. Проведем через них окружность и обозначим через Y вторую точку пересечения с осью Oy. Тогда OA • OB = OC • OY по теореме о двух секущих окружности, проведенных из одной точки, то есть |x1| • |x2| = b² • OY. По теореме Виета |x1| • |x2| = |x1x2| = b². Тогда OY = 1 то есть все окружности проходят через точку (0;1).
Задача 5: Найдите наибольшее значение произведения xy, если:
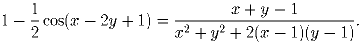
Решение: Пусть 1 – ½ cos (x – 2y + 1) = A. Очевидно, что ½ ≤ A ≤ 1½). Запишем исходное равенство в виде
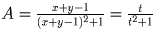 , где t = x + y – 1 и
заметим, что t – корень квадратного
уравнения At² – t + A = 0. Значит это уравнение должно иметь
неотрицательный дискриминант:
1 – 4A² ≥ 0. Отсюда |A| ≤ ½ и, следовательно,
A = ½, cos (x – 2y + 1) = 1. Получили
такую систему:
, где t = x + y – 1 и
заметим, что t – корень квадратного
уравнения At² – t + A = 0. Значит это уравнение должно иметь
неотрицательный дискриминант:
1 – 4A² ≥ 0. Отсюда |A| ≤ ½ и, следовательно,
A = ½, cos (x – 2y + 1) = 1. Получили
такую систему:

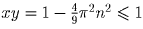 , и максимальное значение произведения xy
равно 1 (достигается при x = y = 1).
, и максимальное значение произведения xy
равно 1 (достигается при x = y = 1).
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1983 >> Районный тур >> 10 класс ФМШ | Убрать решения |